Advantages of Skip List
- The skip list is solid and trustworthy.
- To add a new node to it, it will be inserted extremely quickly.
- Easy to implement compared to the hash table and binary search tree
- The number of nodes in the skip list increases, and the possibility of the worst-case decreases
- Requires only time in the average case for all operations.
- Finding a node in the list is relatively straightforward.
Disadvantages of Skip List
- It needs a greater amount of memory than the balanced tree.
- Reverse search is not permitted.
- Searching is slower than a linked list
- Skip lists are not cache-friendly because they don’t optimize the locality of reference
Deciding nodes level
Each element in the list is represented by a node, the level of the node is chosen randomly while insertion in the list. **Level does not depend on the number of elements in the node.
The level for node is decided by the following algorithm
randomLevel()
lvl := 1
//random() that returns a random value in [0...1)
while random() < p and lvl < MaxLevel do
lvl := lvl + 1
return lvl
MaxLevel is the upper bound on number of levels in the skip list.
- It can be determined as – .
- Above algorithm assure that random level will never be greater than MaxLevel.
- Here is the fraction of the nodes with level pointers
- Also having level pointers and is the number of nodes in the list.
Node Structure
- Each node carries a key and a forward array carrying pointers to nodes of a different level. A level node carries forward pointers indexed through to .

Insertion in Skip List
- We will start from the highest level in the list and compare the key of the next node of the current node with the key to be inserted. The basic idea is If
-
- Key of next node is less than key to be inserted then we keep on moving forward on the same level
-
- Key of next node is greater than the key to be inserted then we store the pointer to current node i at update[i] and move one level down and continue our search.
-
- At the level 0, we will definitely find a position to insert the given key.
Insertion in Skip List Algorithm
Following is the pseudo-code for the insertion algorithm
**Insert(list, searchKey)**
local update[0...MaxLevel+1]
x := list -> header
for i := list -> level downto 0 do
while x -> forward[i] -> key forward[i]
update[i] := x
x := x -> forward[0]
lvl := randomLevel()
if lvl > list -> level then
for i := list -> level + 1 to lvl do
update[i] := list -> header
list -> level := lvl
x := makeNode(lvl, searchKey, value)
for i := 0 to level do
x -> forward[i] := update[i] -> forward[i]
update[i] -> forward[i] := x
Insertion in Skip List Algorithm
- Here holds the pointer to node at level from which we moved down to level and pointer of node left to insertion position at level .
- Consider this example where we want to insert key
Insertion in Skip List Algorithm

Insertion in Skip List in C++
- Following is the code for insertion of key in Skip list
// C++ code for inserting element in skip list
#include <bits/stdc++.h>
using namespace std;
// Class to implement node
class Node
{
public:
int key;
// Array to hold pointers to node of different level
Node **forward;
Node(int, int);
};
...
Insertion in Skip List in C++
Node::Node(int key, int level)
{
this->key = key;
// Allocate memory to forward
forward = new Node*[level+1];
// Fill forward array with 0(NULL)
memset(forward, 0, sizeof(Node*)*(level+1));
};
...
Insertion in Skip List in C++
// Class for Skip list
class SkipList
{
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node *header;
public:
SkipList(int, float);
int randomLevel();
Node* createNode(int, int);
void insertElement(int);
void displayList();
};
...
Insertion in Skip List in C++
SkipList::SkipList(int MAXLVL, float P)
{
this->MAXLVL = MAXLVL;
this->P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
};
...
Insertion in Skip List in C++
// create random level for node
int SkipList::randomLevel()
{
float r = (float)rand()/RAND_MAX;
int lvl = 0;
while (r < P && lvl < MAXLVL)
{
lvl++;
r = (float)rand()/RAND_MAX;
}
return lvl;
};
...
Insertion in Skip List in C++
// create new node
Node* SkipList::createNode(int key, int level)
{
Node *n = new Node(key, level);
return n;
};
...
Insertion in Skip List in C++
// Insert given key in skip list
void SkipList::insertElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for (int i = level; i >= 0; i--)
{
while (current->forward[i] != NULL &&
current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
/* reached level 0 and forward pointer to
right, which is desired position to
insert key.
*/
current = current->forward[0];
...
Insertion in Skip List in C++
...
/* if current is NULL that means we have reached
to end of the level or current's key is not equal
to key to insert that means we have to insert
node between update[0] and current node */
if (current == NULL || current->key != key)
{
// Generate a random level for node
int rlevel = randomLevel();
// If random level is greater than list's current
// level (node with highest level inserted in
// list so far), initialize update value with pointer
// to header for further use
if (rlevel > level)
{
for (int i=level+1;i<rlevel+1;i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level generated
Node* n = createNode(key, rlevel);
// insert node by rearranging pointers
for (int i=0;i<=rlevel;i++)
{
n->forward[i] = update[i]->forward[i];
update[i]->forward[i] = n;
}
cout << "Successfully Inserted key " << key << "\n";
}
};
...
Insertion in Skip List in C++
// Display skip list level wise
void SkipList::displayList()
{
cout<<"\n*****Skip List*****"<<"\n";
for (int i=0;i<=level;i++)
{
Node *node = header->forward[i];
cout << "Level " << i << ": ";
while (node != NULL)
{
cout << node->key<<" ";
node = node->forward[i];
}
cout << "\n";
}
};
...
Insertion in Skip List in C++
// Driver to test above code
int main()
{
// Seed random number generator
srand((unsigned)time(0));
// create SkipList object with MAXLVL and P
SkipList lst(3, 0.5);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
}
Insertion in Skip List in Java
// Java code for inserting element in skip list
class GFG {
// Class to implement node
static class Node {
int key;
// Array to hold pointers to node of different level
Node forward[];
Node(int key, int level)
{
this.key = key;
// Allocate memory to forward
forward = new Node[level + 1];
}
};
...
Insertion in Skip List in Java
// Class for Skip list
static class SkipList {
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node header;
...
Insertion in Skip List in Java
SkipList(int MAXLVL, float P)
{
this.MAXLVL = MAXLVL;
this.P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
}
...
Insertion in Skip List in Java
int randomLevel()
{
float r = (float)Math.random();
int lvl = 0;
while (r < P && lvl < MAXLVL) {
lvl++;
r = (float)Math.random();
}
return lvl;
}
...
Insertion in Skip List in Java
Node createNode(int key, int level)
{
Node n = new Node(key, level);
return n;
}
...
Insertion in Skip List in Java
// Insert given key in skip list
void insertElement(int key)
{
Node current = header;
// create update array and initialize it
Node update[] = new Node[MAXLVL + 1];
/* start from highest level of skip list
move the current pointer forward while
key is greater than key of node next to
current Otherwise inserted current in update
and move one level down and continue search
*/
for (int i = level; i >= 0; i--) {
while (current.forward[i] != null
&& current.forward[i].key < key)
current = current.forward[i];
update[i] = current;
}
/* reached level 0 and forward pointer to
right, which is desired position to
insert key.
*/
current = current.forward[0];
...
Insertion in Skip List in Java
...
/* if current is NULL that means we have reached
to end of the level or current's key is not
equal to key to insert that means we have to
insert node between update[0] and current node
*/
if (current == null || current.key != key) {
// Generate a random level for node
int rlevel = randomLevel();
// If random level is greater than list's
// current level (node with highest level
// inserted in list so far), initialize
// update value with pointer to header for
// further use
if (rlevel > level) {
for (int i = level + 1; i < rlevel + 1;
i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level
// generated
Node n = createNode(key, rlevel);
// insert node by rearranging pointers
for (int i = 0; i <= rlevel; i++) {
n.forward[i] = update[i].forward[i];
update[i].forward[i] = n;
}
System.out.println(
"Successfully Inserted key " + key);
}
}
...
Insertion in Skip List in Java
// Display skip list level wise
void displayList()
{
System.out.println("\n*****Skip List*****");
for (int i = 0; i <= level; i++) {
Node node = header.forward[i];
System.out.print("Level " + i + ": ");
while (node != null) {
System.out.print(node.key + " ");
node = node.forward[i];
}
System.out.println();
}
}
}
...
Insertion in Skip List in Java
// Driver to test above code
public static void main(String[] args)
{
// create SkipList object with MAXLVL and P
SkipList lst = new SkipList(3, 0.5f);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
}
}
// This code is contributed by Lovely Jain
Output
Successfully Inserted key 3
Successfully Inserted key 6
Successfully Inserted key 7
Successfully Inserted key 9
Successfully Inserted key 12
Successfully Inserted key 19
Successfully Inserted key 17
Successfully Inserted key 26
Successfully Inserted key 21
Successfully Inserted key 25
*****Skip List*****
Level 0: 3 6 7 9 12 17 19 21 25 26
Level 1: 3 6 12 17 25 26
Level 2: 3 6 12 25
Level 3: 3 25
Note: The level of nodes is decided randomly, so output may differ.
Time complexity
- Average:
- Worst:
Skip List - Searching and Deletion
Searching an element in Skip list
- Searching an element is very similar to approach for searching a spot for inserting an element in Skip list. The basic idea is if
-
- Key of next node is less than search key then we keep on moving forward on the same level.
-
- Key of next node is greater than the key to be inserted then we store the pointer to current node i at update[i] and move one level down and continue our search.
-
- At the lowest level(0), if the element next to the rightmost element (update[0]) has key equal to the search key, then we have found key otherwise failure. Following is the pseudo code for searching element –
Skip List - Searching Algorithm
**Search(list, searchKey)**
x := list -> header
-- loop invariant: x -> key level downto 0 do
while x -> forward[i] -> key forward[i]
x := x -> forward[0]
if x -> key = searchKey then return x -> value
else return failure
Skip List - Searching Example
- Consider this example where we want to search for key 17-

Deleting an element from the Skip list
- Deletion of an element k is preceded by locating element in the Skip list using above mentioned search algorithm.
- Once the element is located, rearrangement of pointers is done to remove element form list just like we do in singly linked list.
- We start from lowest level and do rearrangement until element next to update[i] is not k. - After deletion of element there could be levels with no elements,
- so we will remove these levels as well by decrementing the level of Skip list.
Skip List - Deletion Algorithm
**Delete(list, searchKey)**
local update[0..MaxLevel+1]
x := list -> header
for i := list -> level downto 0 do
while x -> forward[i] -> key forward[i]
update[i] := x
x := x -> forward[0]
if x -> key = searchKey then
for i := 0 to list -> level do
if update[i] -> forward[i] ≠ x then break
update[i] -> forward[i] := x -> forward[i]
free(x)
while list -> level > 0 and list -> header -> forward[list -> level] = NIL do
list -> level := list -> level – 1
Skip List - Deletion Example
- Consider this example where we want to delete element 6

- Here at level 3, there is no element (arrow in red) after deleting element 6.
- So we will decrement level of skip list by 1.
Skip List - Deletion in C++
// C++ code for searching and deleting element in skip list
#include <bits/stdc++.h>
using namespace std;
// Class to implement node
class Node
{
public:
int key;
// Array to hold pointers to node of different level
Node **forward;
Node(int, int);
};
...
Skip List - Deletion in C++
Node::Node(int key, int level)
{
this->key = key;
// Allocate memory to forward
forward = new Node*[level+1];
// Fill forward array with 0(NULL)
memset(forward, 0, sizeof(Node*)*(level+1));
};
...
Skip List - Deletion in C++
// Class for Skip list
class SkipList
{
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node *header;
...
Skip List - Deletion in C++
...
public:
SkipList(int, float);
int randomLevel();
Node* createNode(int, int);
void insertElement(int);
void deleteElement(int);
void searchElement(int);
void displayList();
};
...
Skip List - Deletion in C++
SkipList::SkipList(int MAXLVL, float P)
{
this->MAXLVL = MAXLVL;
this->P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
};
...
Skip List - Deletion in C++
// create random level for node
int SkipList::randomLevel()
{
float r = (float)rand()/RAND_MAX;
int lvl = 0;
while(r < P && lvl < MAXLVL)
{
lvl++;
r = (float)rand()/RAND_MAX;
}
return lvl;
};
...
Skip List - Deletion in C++
// create new node
Node* SkipList::createNode(int key, int level)
{
Node *n = new Node(key, level);
return n;
};
...
Skip List - Deletion in C++
// Insert given key in skip list
void SkipList::insertElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for(int i = level; i >= 0; i--)
{
while(current->forward[i] != NULL &&
current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
...
Skip List - Deletion in C++
...
/* reached level 0 and forward pointer to
right, which is desired position to
insert key.
*/
current = current->forward[0];
/* if current is NULL that means we have reached
to end of the level or current's key is not equal
to key to insert that means we have to insert
node between update[0] and current node */
if (current == NULL || current->key != key)
{
// Generate a random level for node
int rlevel = randomLevel();
/* If random level is greater than list's current
level (node with highest level inserted in
list so far), initialize update value with pointer
to header for further use */
if(rlevel > level)
{
for(int i=level+1;i<rlevel+1;i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level generated
Node* n = createNode(key, rlevel);
// insert node by rearranging pointers
for(int i=0;i<=rlevel;i++)
{
n->forward[i] = update[i]->forward[i];
update[i]->forward[i] = n;
}
cout<<"Successfully Inserted key "<<key<<"\n";
}
};
...
Skip List - Deletion in C++
// Delete element from skip list
void SkipList::deleteElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for(int i = level; i >= 0; i--)
{
while(current->forward[i] != NULL &&
current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
...
Skip List - Deletion in C++
...
/* reached level 0 and forward pointer to
right, which is possibly our desired node.*/
current = current->forward[0];
// If current node is target node
if(current != NULL and current->key == key)
{
/* start from lowest level and rearrange
pointers just like we do in singly linked list
to remove target node */
for(int i=0;i<=level;i++)
{
/* If at level i, next node is not target
node, break the loop, no need to move
further level */
if(update[i]->forward[i] != current)
break;
update[i]->forward[i] = current->forward[i];
}
// Remove levels having no elements
while(level>0 &&
header->forward[level] == 0)
level--;
cout<<"Successfully deleted key "<<key<<"\n";
}
};
...
Skip List - Deletion in C++
// Search for element in skip list
void SkipList::searchElement(int key)
{
Node *current = header;
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for(int i = level; i >= 0; i--)
{
while(current->forward[i] &&
current->forward[i]->key < key)
current = current->forward[i];
}
/* reached level 0 and advance pointer to
right, which is possibly our desired node*/
current = current->forward[0];
// If current node have key equal to
// search key, we have found our target node
if(current and current->key == key)
cout<<"Found key: "<<key<<"\n";
};
...
Skip List - Deletion in C++
// Display skip list level wise
void SkipList::displayList()
{
cout<<"\n*****Skip List*****"<<"\n";
for(int i=0;i<=level;i++)
{
Node *node = header->forward[i];
cout<<"Level "<<i<<": ";
while(node != NULL)
{
cout<<node->key<<" ";
node = node->forward[i];
}
cout<<"\n";
}
};
...
Skip List - Deletion in C++
// Driver to test above code
int main()
{
// Seed random number generator
srand((unsigned)time(0));
// create SkipList object with MAXLVL and P
SkipList lst(3, 0.5);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
//Search for node 19
lst.searchElement(19);
//Delete node 19
lst.deleteElement(19);
lst.displayList();
}
Output
Successfully Inserted key 3
Successfully Inserted key 6
Successfully Inserted key 7
Successfully Inserted key 9
Successfully Inserted key 12
Successfully Inserted key 19
Successfully Inserted key 17
Successfully Inserted key 26
Successfully Inserted key 21
Successfully Inserted key 25
*****Skip List*****
Level 0: 3 6 7 9 12 17 19 21 25 26
Level 1: 6 9 19 26
Level 2: 19
Found key: 19
Successfully deleted key 19
*****Skip List*****
Level 0: 3 6 7 9 12 17 21 25 26
Level 1: 6 9 26
Time complexity of both searching and deletion (same)
- Time complexity Worst case
- Access –
- Search –
- Insert –
- Space –
- Delete –
Strand Sort
- Geeks for Geeks
Strand Sort
- Strand sort is a recursive sorting algorithm that sorts items of a list into increasing order.
- It has worst time complexity
- which occurs when the input list is reverse sorted.
- It has a best case time complexity of
- which occurs when the input is a list that is already sorted.
Strand Sort Example
- Given a list of items, sort them in increasing order.
- Input:
ip[] = {10, 5, 30, 40, 2, 4, 9}
- Output
op[] = {2, 4, 5, 9, 10, 30, 40}
Strand Sort Example
- Given a list of items, sort them in increasing order.
- Input:
ip[] = {1, 10, 7}
- Output
op[] = {1, 7, 10}
Strand Sort Example
-
Let,
input[] = {10, 5, 30, 40, 2, 4, 9} -
Initialize:
output[] = {}, sublist[] = {}
Strand Sort Example
- Move first item of input to sublist.
sublist[] = {10} - Traverse remaining items of input and if current element is greater than last item of sublist, move this item from input to sublist.
- Now,
sublist[] = {10, 30, 40}, input[] = {5, 2, 4, 9} - Merge sublist into output.
op = {10, 30, 40}
Strand Sort Example
- Next recursive call
- Move first item of input to sublist.
sublist[] = {5}
- Move first item of input to sublist.
- Traverse remaining items of input and move elements greater than last inserted.
input[] = {2, 4}
sublist[] = {5, 9} - Merge sublist into op.
output = {5, 9, 10, 30, 40} - Last Recursive Call
{2, 4}are first moved to sublist and then merged into output.
output = {2, 4, 5, 9, 10, 30, 40}
Steps used in the Strand Sort Algorithm
- Let
ip[]be input list andop[]be output list. - Create an empty sublist and move first item of
ip[]to it. - Traverse remaining items of ip. For every item
x, check ifxis greater than last inserted item to sublist. If yes, removexfromip[]and add at the end of sublist. If no, ignorex(Keep it, it inip[]) - Merge sublist into
op[](output list) - Recur for remaining items in
ip[]and current items inop[].
Strand Sort in C++
// CPP program to implement Strand Sort
#include <bits/stdc++.h>
using namespace std;
// A recursive function to implement Strand
// sort.
// ip is input list of items (unsorted).
// op is output list of items (sorted)
void strandSort(list<int> &ip, list<int> &op)
{
// Base case : input is empty
if (ip.empty())
return;
// Create a sorted sublist with
// first item of input list as
// first item of the sublist
list<int> sublist;
sublist.push_back(ip.front());
ip.pop_front();
...
Strand Sort in C++
...
// Traverse remaining items of ip list
for (auto it = ip.begin(); it != ip.end(); ) {
// If current item of input list
// is greater than last added item
// to sublist, move current item
// to sublist as sorted order is
// maintained.
if (*it > sublist.back()) {
sublist.push_back(*it);
// erase() on list removes an
// item and returns iterator to
// next of removed item.
it = ip.erase(it);
}
// Otherwise ignore current element
else
it++;
}
...
Strand Sort in C++
...
// Merge current sublist into output
op.merge(sublist);
...
Strand Sort in C++
// Recur for remaining items in
// input and current items in op.
strandSort(ip, op);
} //end of function...
Strand Sort in C++
// Driver code
int main(void)
{
list<int> ip{10, 5, 30, 40, 2, 4, 9};
// To store sorted output list
list<int> op;
// Sorting the list
strandSort(ip, op);
// Printing the sorted list
for (auto x : op)
cout << x << " ";
return 0;
}
Strand Sort in C
Sorting algorithms/Strand sort - Rosetta Code
#include <stdio.h>
typedef struct node_t *node, node_t;
struct node_t { int v; node next; };
typedef struct { node head, tail; } slist;
...
Strand Sort in C
void push(slist *l, node e) {
if (!l->head) l->head = e;
if (l->tail) l->tail->next = e;
l->tail = e;
}
...
Strand Sort in C
node removehead(slist *l) {
node e = l->head;
if (e) {
l->head = e->next;
e->next = 0;
}
return e;
}
...
Strand Sort in C
void join(slist *a, slist *b) {
push(a, b->head);
a->tail = b->tail;
}
...
Strand Sort in C
void merge(slist *a, slist *b) {
slist r = {0};
while (a->head && b->head)
push(&r, removehead(a->head->v <= b->head->v ? a : b));
join(&r, a->head ? a : b);
*a = r;
b->head = b->tail = 0;
}
...
Strand Sort in C
void sort(int *ar, int len)
{
node_t all[len];
// array to list
for (int i = 0; i < len; i++)
all[i].v = ar[i], all[i].next = i < len - 1 ? all + i + 1 : 0;
slist list = {all, all + len - 1}, rem, strand = {0}, res = {0};
for (node e = 0; list.head; list = rem) {
rem.head = rem.tail = 0;
while ((e = removehead(&list)))
push((!strand.head || e->v >= strand.tail->v) ? &strand : &rem, e);
merge(&res, &strand);
}
// list to array
for (int i = 0; res.head; i++, res.head = res.head->next)
ar[i] = res.head->v;
}
...
Strand Sort in C
void show(const char *title, int *x, int len)
{
printf("%s ", title);
for (int i = 0; i < len; i++)
printf("%3d ", x[i]);
putchar('\n');
}
...
Strand Sort in C
# define SIZE sizeof(x)/sizeof(int)
int main(void)
{
int x[] = {-2,0,-2,5,5,3,-1,-3,5,5,0,2,-4,4,2};
show("before sort:", x, SIZE);
sort(x, sizeof(x)/sizeof(int));
show("after sort: ", x, SIZE);
return 0;
}
Arrays
What is an Array?
- Whenever we want to work with large number of data values,
- we need to use that much number of different variables.
- As the number of variables are increasing,
- complexity of the program also increases and programmers get confused with the variable names.
- There may be situations in which we need to work with large number of similar data values. - To make this work more easy, C programming language provides a concept called "Array".
What is an Array?
An array is a variable which can store multiple values of same data type at a time.
An array can also be defined as follows...
"Collection of similar data items stored in continuous memory locations with single name".
To understand the concept of arrays, consider the following example declaration.
What is an Array?
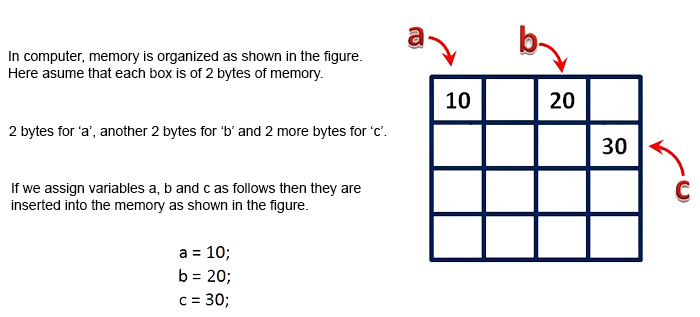
int a, b, c
- Here, the compiler allocates 2 bytes of memory with name 'a', another 2 bytes of memory with name 'b' and more 2 bytes with name 'c'.
- These three memory locations are may be in sequence or may not be in sequence. Here these individual variables store only one value at a time.
- Now consider the following declaration...
What is an Array?
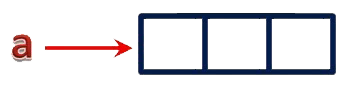
int a[3];
- Here, the compiler allocates total 6 bytes of continuous memory locations with single name 'a'. But allows to store three different integer values (each in 2 bytes of memory) at a time.
What is an Array?
- And memory is organized as follows
What is an Array?
- That means all these three memory locations are named as 'a'.
- But "how can we refer individual elements?" is the big question.
- Answer for this question is, compiler not only allocates memory,
- but also assigns a numerical value to each individual element of an array.
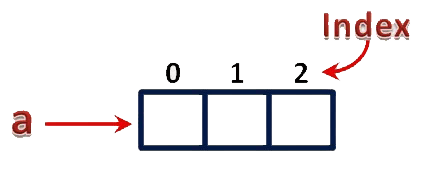
- This numerical value is called as "
Index".
What is an Array?
Indexvalues for the above example are as follows...
What is an Array?
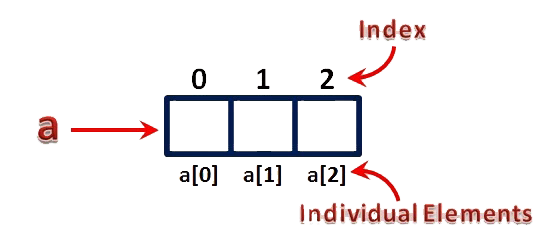
- The individual elements of an array are identified using the combination of
nameandindexas follows...arrayName[indexValue]
- For the above example, the individual elements can be referred as follows...
What is an Array?
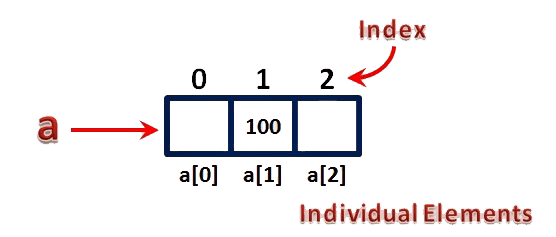
If I want to assign a value to any of these memory locations (array elements), we can assign as follows...
- a[1] = 100;
The result will be as follows...
Types of Arrays in C
- In c programming language, arrays are classified into two types. They are as follows...
-
- Single Dimensional Array / One Dimensional Array
-
- Multi Dimensional Array
-
Single Dimensional Array
- In c programming language,
- single dimensional arrays are used to store list of values of same datatype.
- In other words, single dimensional arrays are used to store a row of values.
- In single dimensional array, data is stored in linear form.
- Single dimensional arrays are also called as
- one-dimensional arrays,
- Linear Arrays or simply
- 1-D Arrays.
Declaration of Single Dimensional Array
- We use the following general syntax for declaring a single dimensional array...
datatype arrayName [ size ] ;
int rollNumbers [60] ;
The above declaration of single dimensional array reserves 60 continuous memory locations of 2 bytes each with the name rollNumbers and tells the compiler to allow only integer values into those memory locations.
Initialization of Single Dimensional Array
- We use the following general syntax for declaring and initializing a single dimensional array with size and initial values.
datatype arrayName [ size ] = {value1, value2, ...} ;
int marks [6] = { 89, 90, 76, 78, 98, 86 } ;
- The above declaration of single dimensional array reserves 6 contiguous memory locations of 2 bytes each with the name marks and initializes with value
89in first memory location,90in second memory location,76in third memory location,78in fourth memory location,98in fifth memory location and86in sixth memory location.
Initialization of Single Dimensional Array
- We can also use the following general syntax to intialize a single dimensional array without specifying size and with initial values.
datatype arrayName [ ] = {value1, value2, ...} ;
The array must be initialized if it is created without specifying any size. In this case, the size of the array is decided based on the number of values initialized
Initialization of Single Dimensional Array
int marks [] = { 89, 90, 76, 78, 98, 86 } ;
char studentName [] = "btechsmartclass";
- In the above example declaration, size of the array
marksis6and the size of the arraystudentNameis16. - This is because in case of character array, compiler stores one exttra character called
\0(NULL)at the end.
Accessing Elements of Single Dimensional Array
- In c programming language, to access the elements of single dimensional array we use array name followed by index value of the element that to be accessed.
- Here the index value must be enclosed in square braces.
Indexvalue of an element in an array is the reference number given to each element at the time of memory allocation.- The index value of single dimensional array starts with zero (0) for first element and incremented by one for each element.
- The index value in an array is also called as
subscriptorindices.
Accessing Elements of Single Dimensional Array
- We use the following general syntax to access individual elements of single dimensional array...
arrayName [ indexValue ]
marks [2] = 99 ;
- In the above statement, the third element of 'marks' array is assinged with value '99'.
Multi Dimensional Array
- An array of arrays is called as multi dimensional array.
- In simple words, an array created with more than one dimension (size) is called as multi dimensional array.
- Multi dimensional array can be of two dimensional array or three dimensional array or four dimensional array or more
- Most popular and commonly used multi dimensional array is two dimensional array. The 2-D arrays are used to store data in the form of table.
- We also use 2-D arrays to create mathematical matrices.
Declaration of Two Dimensional Array
- We use the following general syntax for declaring a two dimensional array
datatype arrayName [ rowSize ] [ columnSize ] ;
int matrix_A [2][3] ;
- The above declaration of two dimensional array reserves 6 continuous memory locations of 2 bytes each in the form of 2 rows and 3 columns.
Initialization of Two Dimensional Array
- We use the following general syntax for declaring and initializing a two dimensional array with specific number of rows and coloumns with initial values
datatype arrayName [rows][colmns] = {
{r1c1value, r1c2value, ...},
{r2c1,r2c2,...}
...} ;
int matrix_A [2][3] = { {1, 2, 3},{4, 5, 6} } ;
- The above declaration of two-dimensional array reserves 6 contiguous memory locations of 2 bytes each in the form of 2 rows and 3 columns.
- And the first row is initialized with values 1, 2 & 3 and second row is initialized with values 4, 5 & 6.
Initialization of Two Dimensional Array
We can also initialize as follows...
int matrix_A [2][3] = {
{1, 2, 3},
{4, 5, 6}
} ;
Accessing Individual Elements of Two Dimensional Array
- In a c programming language, to access elements of a two-dimensional array we use array name followed by row index value and column index value of the element that to be accessed.
- Here the row and column index values must be enclosed in separate square braces.
- In case of the two-dimensional array the compiler assigns separate index values for rows and columns.
- We use the following general syntax to access the individual elements of a two-dimensional array...
arrayName [ rowIndex ] [ columnIndex ]
matrix_A [0][1] = 10 ;
- In the above statement, the element with row index 0 and column index 1 of matrix_A array is assinged with value 10.
Circular Array
Circular Array
An example problem :
Suppose n people are sitting at a circular table with names A, B, C, D, ... Given a name, we need to print all n people (in order) starting from the given name.
Circular Array
-
For example, consider people and given name as . People sitting in a circular manner starting from are .
-
A simple solution is to create an auxiliary array of size and store it in another array. For example for people, we create below the auxiliary array.
-
-
Now for any given index, we simply print n elements starting from it. For example, we print the following .
-
A B C D E F A B C D E F
-
Below is the implementation of the above approach.
Circular Array in C++
// CPP program to demonstrate use of circular
// array using extra memory space
#include <bits/stdc++.h>
using namespace std;
void print(char a[], int n, int ind)
{
// Create an auxiliary array of twice size.
char b[(2 * n)];
// Copy a[] to b[] two times
for (int i = 0; i < n; i++)
b[i] = b[n + i] = a[i];
// print from ind-th index to (n+i)th index.
for (int i = ind; i < n + ind; i++)
cout << b[i] << " ";
}
Circular Array in C++
// Driver code
int main()
{
char a[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
int n = sizeof(a) / sizeof(a[0]);
print(a, n, 3);
return 0;
}
Circular Array in Java
// Java program to demonstrate use of circular
// array using extra memory space
import java.util.*;
import java.lang.*;
public class GfG{
public static void print(char a[], int n,
int ind){
// Create an auxiliary array
// of twice size.
char[] b = new char[(2 * n)];
// Copy a[] to b[] two times
for (int i = 0; i < n; i++)
b[i] = b[n + i] = a[i];
// print from ind-th index to
// (n+i)th index.
for (int i = ind; i < n + ind; i++)
System.out.print(b[i]+" ");
}
...
Circular Array in Java
...
// Driver code
public static void main(String argc[]){
char[] a = new char[]{ 'A', 'B', 'C',
'D', 'E', 'F' };
int n = 6;
print(a, n, 3);
}
}
/* This code is contributed by Sagar Shukla */
Circular Array in C#
// C# program to demonstrate use of circular
// array using extra memory space
using System;
public class GfG {
public static void print(char[] a, int n,
int ind)
{
// Create an auxiliary array
// of twice size.
char[] b = new char[(2 * n)];
// Copy a[] to b[] two times
for (int i = 0; i < n; i++)
b[i] = b[n + i] = a[i];
// print from ind-th index to
// (n+i)th index.
for (int i = ind; i < n + ind; i++)
Console.Write(b[i] + " ");
}
Circular Array in C#
...
// Driver code
public static void Main()
{
char[] a = new char[] { 'A', 'B', 'C',
'D', 'E', 'F' };
int n = 6;
print(a, n, 3);
}
}
/* This code is contributed by vt_m*/
Array Rotations
- Geeks for Geeks
Array Rotations
- Given an array of integers
arr[]of sizeNand an integer, the task is to rotate the array elements to theleftbydpositions.
Array Rotations - Example
Input
arr[] = {1, 2, 3, 4, 5, 6, 7},d = 2
Output
3 4 5 6 7 1 2
Array Rotations - Example
Input:
arr[] = {3, 4, 5, 6, 7, 1, 2}, d=2
Output:
5 6 7 1 2 3 4
Array Rotations
Approach 1 (Using temp array)
- This problem can be solved using the below idea:
- After rotating d positions to the left,
- the first d elements become the last d elements of the array
- First store the elements from index d to N-1 into the temp array.
- Then store the first d elements of the original array into the temp array.
- Copy back the elements of the temp array into the original array
Array Rotations
- Suppose the give array is arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2.
- First Step:
- => Store the elements from 2nd index to the last.
- => temp[] = [3, 4, 5, 6, 7]
- Second Step:
- => Now store the first 2 elements into the temp[] array.
- => temp[] = [3, 4, 5, 6, 7, 1, 2]
- Third Steps:
- => Copy the elements of the temp[] array into the original array.
- => arr[] = temp[] So arr[] = [3, 4, 5, 6, 7, 1, 2]
Follow the steps below to solve the given problem.
Array Rotations
- Initialize a temporary array(temp[n]) of length same as the original array
- Initialize an integer(k) to keep a track of the current index
- Store the elements from the position d to n-1 in the temporary array
- Now, store 0 to d-1 elements of the original array in the temporary array
- Lastly, copy back the temporary array to the original array
Array Rotations in C++
#include <bits/stdc++.h>
using namespace std;
// Fuction to rotate array
void Rotate(int arr[], int d, int n)
{
// Storing rotated version of array
int temp[n];
// Keepig track of the current index
// of temp[]
int k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++) {
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++) {
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
...
Array Rotations in C++
// Function to print elements of array
void PrintTheArray(int arr[], int n)
{
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
}
...
Array Rotations in C++
// Driver code
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int N = sizeof(arr) / sizeof(arr[0]);
int d = 2;
// Function calling
Rotate(arr, d, N);
PrintTheArray(arr, N);
return 0;
}
Array Rotations in Java
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
// Fuction to rotate array
static void Rotate(int arr[], int d, int n)
{
// Storing rotated version of array
int temp[] = new int[n];
// Keepig track of the current index
// of temp[]
int k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++) {
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++) {
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
...
Array Rotations in Java
// Function to print elements of array
static void PrintTheArray(int arr[], int n)
{
for (int i = 0; i < n; i++) {
System.out.print(arr[i]+" ");
}
}
public static void main (String[] args) {
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int N = arr.length;
int d = 2;
// Function calling
Rotate(arr, d, N);
PrintTheArray(arr, N);
}
}
Array Rotations in C#
// Include namespace system
using System;
public class GFG
{
// Fuction to rotate array
public static void Rotate(int[] arr, int d, int n)
{
// Storing rotated version of array
int[] temp = new int[n];
// Keepig track of the current index
// of temp[]
var k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++)
{
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++)
{
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++)
{
arr[i] = temp[i];
}
}
...
Array Rotations in C#
// Function to print elements of array
public static void PrintTheArray(int[] arr, int n)
{
for (int i = 0; i < n; i++)
{
Console.Write(arr[i].ToString() + " ");
}
}
...
Array Rotations in C#
public static void Main(String[] args)
{
int[] arr = {1, 2, 3, 4, 5, 6, 7};
var N = arr.Length;
var d = 2;
// Function calling
GFG.Rotate(arr, d, N);
GFG.PrintTheArray(arr, N);
}
}
Arrangement Rearrangement
- Geeks for Geeks
Arrangement Rearrangement
- Rearrange an array such that
arr[i] = i - Given an array of elements of length
N, ranging from0toN – 1. - All elements may not be present in the array.
- If the element is not present then there will be
-1present in the array. - Rearrange the array such that
A[i] = iand ifiis not present,- display
-1at that place.
- display
Arrangement Rearrangement - Example
- Input :
arr = {-1, -1, 6, 1, 9, 3, 2, -1, 4, -1} - Output :
[-1, 1, 2, 3, 4, -1, 6, -1, -1, 9]
Arrangement Rearrangement - Example
- Input :
arr = {19, 7, 0, 3, 18, 15, 12, 6, 1, 8, 11, 10, 9, 5, 13, 16, 2, 14, 17, 4} - Output :
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
Arrangement Rearrangement - Naive Approach
- Navigate the numbers from 0 to n-1.
- Now navigate through array.
- If (i==a[j]) , then replace the element at i position with a[j] position.
- If there is any element in which -1 is used instead of the number then it will be replaced automatically.
- Now, iterate through the array and check if (a[i]!=i) , if it s true then replace a[i] with -1.
Arrangement Rearrangement in C
// C program for above approach
#include <stdio.h>
// Function to transform the array
void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i) {
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
Arrangement Rearrangement in C
...
// Iterate over array
for (i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
Arrangement Rearrangement in C
...
// Print the output
printf("Array after Rearranging\n");
for (i = 0; i < n; i++) {
printf("%d ",ar[i]);
}
}
...
Arrangement Rearrangement in C
// Driver Code
int main()
{
int n, ar[] = { -1, -1, 6, 1, 9, 3, 2, -1, 4, -1 };
n = sizeof(ar) / sizeof(ar[0]);
// Function Call
fixArray(ar, n);
}
Arrangement Rearrangement in C++
// C++ program for above approach
#include <iostream>
using namespace std;
// Function to transform the array
void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i) {
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
Arrangement Rearrangement in C++
// Iterate over array
for (i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
Arrangement Rearrangement in C++
...
// Print the output
cout << "Array after Rearranging" << endl;
for (i = 0; i < n; i++) {
cout << ar[i] << " ";
}
}
...
Arrangement Rearrangement in C++
...
// Driver Code
int main()
{
int n, ar[] = { -1, -1, 6, 1, 9, 3, 2, -1, 4, -1 };
n = sizeof(ar) / sizeof(ar[0]);
// Function Call
fixArray(ar, n);
}
Arrangement Rearrangement in Java
// Java program for above approach
class GFG{
// Function to transform the array
public static void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for(i = 0; i < n; i++)
{
for(j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i)
{
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
Arrangement Rearrangement in Java
...
// Iterate over array
for(i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
Arrangement Rearrangement in Java
...
// Print the output
System.out.println("Array after Rearranging");
for(i = 0; i < n; i++)
{
System.out.print(ar[i] + " ");
}
}
...
Arrangement Rearrangement in Java
...
// Driver Code
public static void main(String[] args)
{
int n, ar[] = { -1, -1, 6, 1, 9,
3, 2, -1, 4, -1 };
n = ar.length;
// Function Call
fixArray(ar, n);
}
}
Arrangement Rearrangement in C#
// C# program for above approach
using System;
class GFG {
// Function to transform the array
static void fixArray(int[] ar, int n)
{
int i, j, temp;
// Iterate over the array
for(i = 0; i < n; i++)
{
for(j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i)
{
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
// Iterate over array
for(i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
// Print the output
Console.WriteLine("Array after Rearranging");
for(i = 0; i < n; i++)
{
Console.Write(ar[i] + " ");
}
}
...
Arrangement Rearrangement in C#
static void Main() {
int[] ar = { -1, -1, 6, 1, 9,
3, 2, -1, 4, -1 };
int n = ar.Length;
// Function Call
fixArray(ar, n);
}
}
// This code is contributed by divyeshrabadiya07
Array Searching and Sorting
Difference between Searching and Sorting Algorithm
| S.No. | Searching Algorithm | Sorting Algorithm |
|---|---|---|
| 1. | Searching Algorithms are designed to retrieve an element from any data structure where it is used. | A Sorting Algorithm is used to arranging the data of list or array into some specific order. |
| 2. | These algorithms are generally classified into two categories i.e. Sequential Search and Interval Search. | There are two different categories in sorting. These are Internal and External Sorting. |
| 3. | The worst-case time complexity of searching algorithm is O(N). | The worst-case time complexity of many sorting algorithms like Bubble Sort, Insertion Sort, Selection Sort, and Quick Sort is O(N2). |
| 4. | There is no stable and unstable searching algorithms. | Bubble Sort, Insertion Sort, Merge Sort etc are the stable sorting algorithms whereas Quick Sort, Heap Sort etc are the unstable sorting algorithms. |
| 5. | The Linear Search and the Binary Search are the examples of Searching Algorithms. | The Bubble Sort, Insertion Sort, Selection Sort, Merge Sort, Quick Sort etc are the examples of Sorting Algorithms. |
Matrix
Matrix Rotation - Examples
- Given a matrix, clockwise rotate elements in it
- Input
1 2 3
4 5 6
7 8 9
- Output
4 1 2
7 5 3
8 9 6
Matrix Rotation - Examples
For 4*4 matrix
- Input
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
Output:
5 1 2 3
9 10 6 4
13 11 7 8
14 15 16 12
Matrix Rotation - Examples
- The idea is to use loops similar to the program for printing a matrix in spiral form.
- One by one rotate all rings of elements, starting from the outermost.
- To rotate a ring, we need to do following.
-
- Move elements of top row.
-
- Move elements of last column.
-
- Move elements of bottom row.
-
- Move elements of first column.
-
- Repeat above steps for inner ring while there is an inner ring.
Matrix Rotation in C++
// C++ program to rotate a matrix
#include <bits/stdc++.h>
#define R 4
#define C 4
using namespace std;
...
Matrix Rotation in C++
...
// A function to rotate a matrix mat[][] of size R x C.
// Initially, m = R and n = C
void rotatematrix(int m, int n, int mat[R][C])
{
int row = 0, col = 0;
int prev, curr;
/*
row - Starting row index
m - ending row index
col - starting column index
n - ending column index
i - iterator
*/
while (row < m && col < n)
{
if (row + 1 == m || col + 1 == n)
break;
// Store the first element of next row, this
// element will replace first element of current
// row
prev = mat[row + 1][col];
/* Move elements of first row from the remaining rows */
for (int i = col; i < n; i++)
{
curr = mat[row][i];
mat[row][i] = prev;
prev = curr;
}
row++;
/* Move elements of last column from the remaining columns */
for (int i = row; i < m; i++)
{
curr = mat[i][n-1];
mat[i][n-1] = prev;
prev = curr;
}
n--;
/* Move elements of last row from the remaining rows */
if (row < m)
{
for (int i = n-1; i >= col; i--)
{
curr = mat[m-1][i];
mat[m-1][i] = prev;
prev = curr;
}
}
m--;
/* Move elements of first column from the remaining rows */
if (col < n)
{
for (int i = m-1; i >= row; i--)
{
curr = mat[i][col];
mat[i][col] = prev;
prev = curr;
}
}
col++;
}
...
Matrix Rotation in C++
...
// Print rotated matrix
for (int i=0; i<R; i++)
{
for (int j=0; j<C; j++)
cout << mat[i][j] << " ";
cout << endl;
}
}
Matrix Rotation in C++
/* Driver program to test above functions */
int main()
{
// Test Case 1
int a[R][C] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
// Test Case 2
/* int a[R][C] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
*/
rotatematrix(R, C, a);
return 0;
}
Matrix Rotation in Java
// Java program to rotate a matrix
import java.lang.*;
import java.util.*;
class GFG
{
static int R = 4;
static int C = 4;
// A function to rotate a matrix
// mat[][] of size R x C.
// Initially, m = R and n = C
static void rotatematrix(int m,
int n, int mat[][])
{
int row = 0, col = 0;
int prev, curr;
/*
row - Starting row index
m - ending row index
col - starting column index
n - ending column index
i - iterator
*/
while (row < m && col < n)
{
if (row + 1 == m || col + 1 == n)
break;
// Store the first element of next
// row, this element will replace
// first element of current row
prev = mat[row + 1][col];
// Move elements of first row
// from the remaining rows
for (int i = col; i < n; i++)
{
curr = mat[row][i];
mat[row][i] = prev;
prev = curr;
}
row++;
// Move elements of last column
// from the remaining columns
for (int i = row; i < m; i++)
{
curr = mat[i][n-1];
mat[i][n-1] = prev;
prev = curr;
}
n--;
// Move elements of last row
// from the remaining rows
if (row < m)
{
for (int i = n-1; i >= col; i--)
{
curr = mat[m-1][i];
mat[m-1][i] = prev;
prev = curr;
}
}
m--;
// Move elements of first column
// from the remaining rows
if (col < n)
{
for (int i = m-1; i >= row; i--)
{
curr = mat[i][col];
mat[i][col] = prev;
prev = curr;
}
}
col++;
}
// Print rotated matrix
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
System.out.print( mat[i][j] + " ");
System.out.print("\n");
}
}
Matrix Rotation in Java
/* Driver program to test above functions */
public static void main(String[] args)
{
// Test Case 1
int a[][] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
// Test Case 2
/* int a[][] = new int {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};*/
rotatematrix(R, C, a);
}
}
Matrix Rotation in C#
// C# program to rotate a matrix
using System;
class GFG {
static int R = 4;
static int C = 4;
// A function to rotate a matrix
// mat[][] of size R x C.
// Initially, m = R and n = C
static void rotatematrix(int m,
int n, int [,]mat)
{
int row = 0, col = 0;
int prev, curr;
/*
row - Starting row index
m - ending row index
col - starting column index
n - ending column index
i - iterator
*/
while (row < m && col < n)
{
if (row + 1 == m || col + 1 == n)
break;
// Store the first element of next
// row, this element will replace
// first element of current row
prev = mat[row + 1, col];
// Move elements of first row
// from the remaining rows
for (int i = col; i < n; i++)
{
curr = mat[row,i];
mat[row, i] = prev;
prev = curr;
}
row++;
// Move elements of last column
// from the remaining columns
for (int i = row; i < m; i++)
{
curr = mat[i,n-1];
mat[i, n-1] = prev;
prev = curr;
}
n--;
// Move elements of last row
// from the remaining rows
if (row < m)
{
for (int i = n-1; i >= col; i--)
{
curr = mat[m-1,i];
mat[m-1,i] = prev;
prev = curr;
}
}
m--;
// Move elements of first column
// from the remaining rows
if (col < n)
{
for (int i = m-1; i >= row; i--)
{
curr = mat[i,col];
mat[i,col] = prev;
prev = curr;
}
}
col++;
}
// Print rotated matrix
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
Console.Write( mat[i,j] + " ");
Console.Write("\n");
}
}
Matrix Rotation in C#
/* Driver program to test above functions */
public static void Main()
{
// Test Case 1
int [,]a = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
// Test Case 2
/* int a[][] = new int {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};*/
rotatematrix(R, C, a);
}
}
// This code is contributed by nitin mittal.
Sparse Matrix
- Geeks for Geeks
What is Sparse Matrix?
- In computer programming, a matrix can be defined with a 2-dimensional array.
- Any array with 'm' columns and 'n' rows represent a m X n matrix.
- There may be a situation in which a matrix contains more number of ZERO values than NON-ZERO values.
- Such matrix is known as sparse matrix.
- Sparse matrix is a matrix which contains very few non-zero elements.
What is Sparse Matrix?
- When a sparse matrix is represented with a 2-dimensional array,
- we waste a lot of space to represent that matrix.
- For example, consider a matrix of size 100 X 100 containing only 10 non-zero elements. In this matrix,
- only 10 spaces are filled with non-zero values and remaining spaces of the matrix are filled with zero.
- That means, totally we allocate 100 X 100 X 2 = 20000 bytes of space to store this integer matrix.
- And to access these 10 non-zero elements we have to make scanning for 10000 times.
- we waste a lot of space to represent that matrix.
- To make it simple we use the following sparse matrix representation.
Sparse Matrix Representations
- A sparse matrix can be represented by using TWO representations, those are as follows
- Triplet Representation (Array Representation)
- Linked Representation
Sparse Matrix - Triplet Representation (Array Representation)
- In this representation, we consider only non-zero values along with their row and column index values.
- In this representation, the 0th row stores the total number of rows,
- total number of columns and the total number of non-zero values in the sparse matrix.
Sparse Matrix - Triplet Representation (Array Representation)
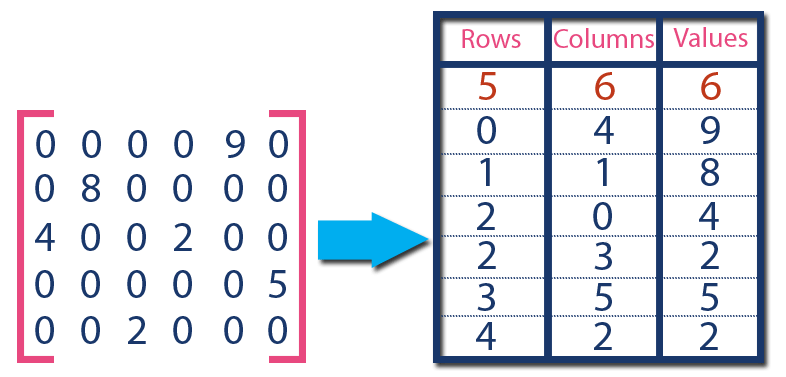
- For example, consider a matrix of size
5 x 6containing6number of non-zero values. This matrix can be represented as shown in the image
Sparse Matrix - Triplet Representation (Array Representation)
- In above example matrix, there are only
6non-zero elements ( those are9, 8, 4, 2, 5 & 2) and matrix size is5 X 6. - We represent this matrix as shown in the above image.
- Here the first row in the right side table is filled with values 5, 6 & 6 which indicates that it is a sparse matrix with
5rows,6columns &6non-zero values. - The second row is filled with
0, 4, & 9which indicates the non-zero value 9 is at the 0th-row 4th column in the Sparse matrix. - In the same way, the remaining non-zero values also follow a similar pattern.
Sparse Matrix - Triplet Representation (Array Representation) in C++
#include<iostream>
using namespace std;
int main()
{
// sparse matrix of class 5x6 with 6 non-zero values
int sparseMatrix[5][6] =
{
{0 , 0 , 0 , 0 , 9, 0 },
{0 , 8 , 0 , 0 , 0, 0 },
{4 , 0 , 0 , 2 , 0, 0 },
{0 , 0 , 0 , 0 , 0, 5 },
{0 , 0 , 2 , 0 , 0, 0 }
};
...
Sparse Matrix - Triplet Representation (Array Representation) in C++
...
// Finding total non-zero values in the sparse matrix
int size = 0;
for (int row = 0; row < 5; row++)
for (int column = 0; column < 6; column++)
if (sparseMatrix[row][column] != 0)
size++;
...
Sparse Matrix - Triplet Representation (Array Representation) in C++
...
// Defining result Matrix
int resultMatrix[3][size];
// Generating result matrix
int k = 0;
for (int row = 0; row < 5; row++)
for (int column = 0; column < 6; column++)
if (sparseMatrix[row][column] != 0)
{
resultMatrix[0][k] = row;
resultMatrix[1][k] = column;
resultMatrix[2][k] = sparseMatrix[row][column];
k++;
}
...
Sparse Matrix - Triplet Representation (Array Representation) in C++
...
// Displaying result matrix
cout<<"Triplet Representation : "<<endl;
for (int row=0; row<3; row++)
{
for (int column = 0; column<size; column++)
cout<<resultMatrix[row][column]<<" ";
cout<<endl;
}
return 0;
}
Output
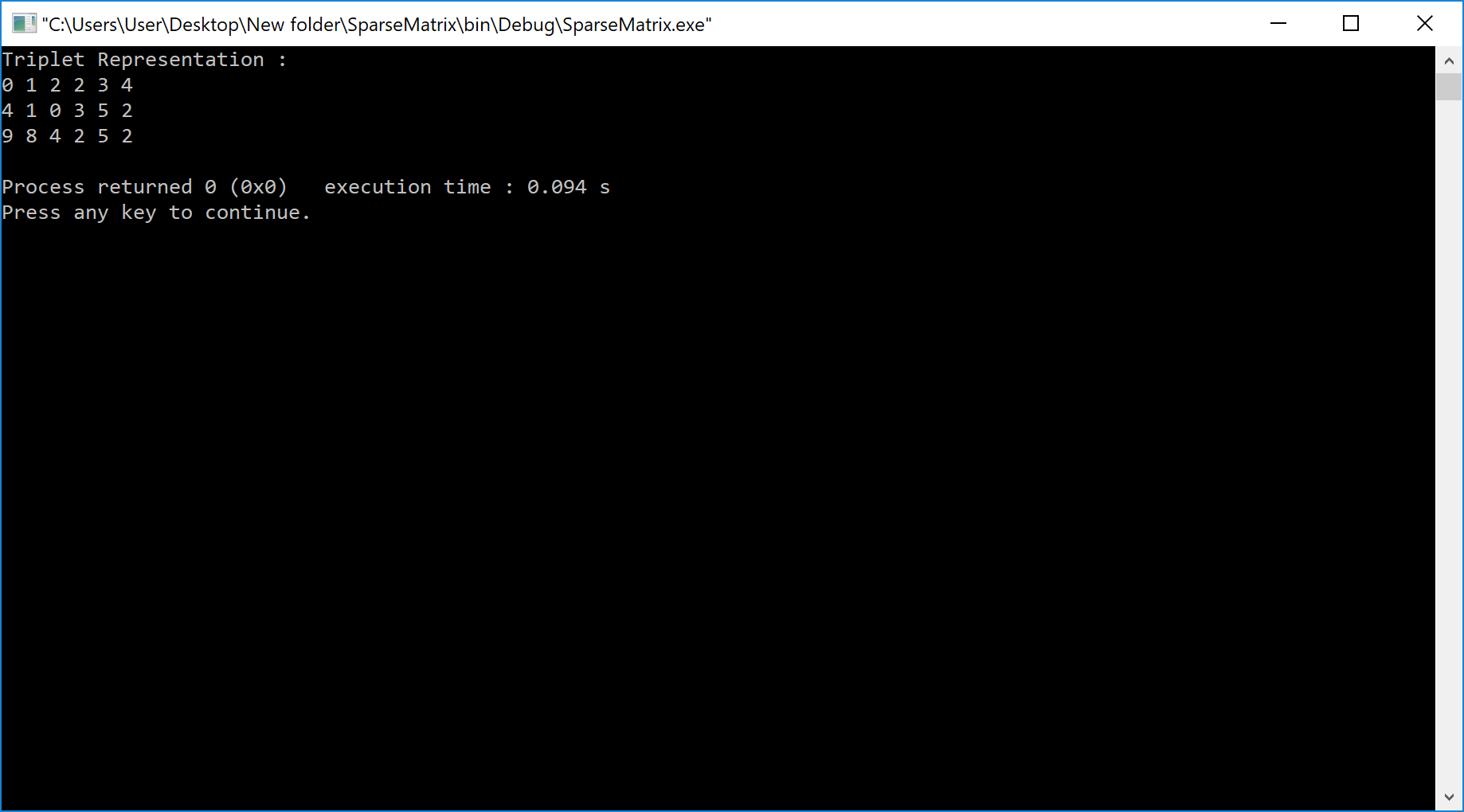
Sparse Matrix - Linked List Representation
- In linked representation, we use a linked list data structure to represent a sparse matrix.
- In this linked list, we use two different nodes namely header node and element node.
Sparse Matrix - Linked List Representation
- Header node consists of three fields and element node consists of five fields as shown in the image

Sparse Matrix - Linked List Representation
- Consider the above same sparse matrix used in the Triplet representation. This sparse matrix can be represented using linked representation as shown in the below image...
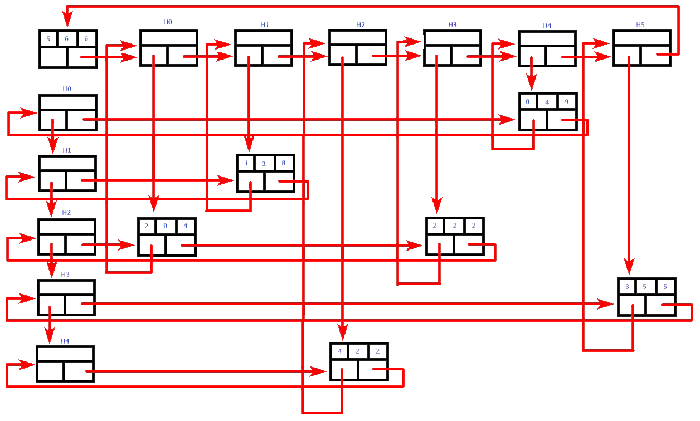
Sparse Matrix - Linked List Representation
- In the above representation,
H0, H1,..., H5indicates the header nodes which are used to represent indexes. - Remaining nodes are used to represent non-zero elements in the matrix,
- except the very first node which is used to represent abstract information of the sparse matrix (i.e., It is a matrix of 5 X 6 with 6 non-zero elements).
- In this representation, in each row and column, the last node right field points to its respective header node.
