CE205 Data Structures¶
Week-2¶
Linked Lists and Related Algorithms Arrays and Matrices¶
Download PDF,DOCX, SLIDE, PPTX
Outline-1¶
- Resources
- ASN.1 C Workshop
- Single Linked List
- Circular Linked List
- Double Linked List
- XOR Linked List
- Skip List
- Strand Sort
Outline-2¶
- Arrays
- Array Rotations
- Arrangement Rearrangement
- Array Searching and Sorting
- Matrix
- Sparse Matrix
Resources¶
- WilliamFiset
- WilliamFiset - YouTube
- GitHub - williamfiset/Algorithms: A collection of algorithms and data structures
- Btech Smart Class
- Data Structures Tutorials - Introduction to Algorithms
- Programiz
- Data Structure and Types
- GeeksforGeeks
- Array Data Structure - GeeksforGeeks
- Visual Algo
- https://visualgo.net/en
Workshop¶
Follow the link below and complete steps.
There are quick start and reference guides
- http://lionet.info/asn1c/asn1c-quick.pdf
- http://lionet.info/asn1c/asn1c-usage.pdf
- https://www.itu.int/ITU-T/studygroups/com17/languages/
Workshop¶
Visit TÜBİTAK KAMU SM MA3API Web Page
Workshop¶
Check out ASN.1 encoded standards.
- ETSI TS 101 733 CADES digital signature (ASN data structure)
- https://www.etsi.org/deliver/etsi_ts/101700_101799/101733/02.02.01_60/ts_101733v020201p.pdf
- ETSI TS 102 778 PADES digital signature (PDF data structure)
- https://www.etsi.org/deliver/etsi_ts/102700_102799/10277803/01.02.01_60/ts_10277803v010201p.pdf
- ETSI TS 101 903 XADES digital signature (XML data structure)
- https://www.etsi.org/deliver/etsi_ts/101900_101999/101903/01.04.02_60/ts_101903v010402p.pdf
- ETSI TS 102 918 ASiC digital signature
- https://www.etsi.org/deliver/etsi_ts/102900_102999/102918/01.03.01_60/ts_102918v010301p.pdf
Workshop¶
Check out ASN.1 encoded standards.
- Also there is An Implementation of CAdES, XAdES, PAdES and ASiC for Windows in C++
- https://github.com/WindowsNT/AdES
Workshop¶
Telecom Standard Example for ASN.1
Workshop¶
Industrial Data Standards - Payment¶
- TLV Utilities
- https://paymentcardtools.com/
- https://emvlab.org/dumpasn1/
- Sample EMV ASN.1
- https://github.com/mmattice/emv-asn1
Workshop¶
Industrial Data Standards - Telco¶
ASN.1 Standartları¶
- ETSI
- https://portal.etsi.org/Services/Centre-for-Testing-Interoperability/ETSI-Approach/Specification-Languages/ASN1
- ITU-T
- https://www.itu.int/ITU-T/recommendations/fl.aspx?lang=1
- ASN.1 Book
- https://www.oss.com/asn1/resources/books-whitepapers-pubs/dubuisson-asn1-book.PDF
Workshop¶
Network Measurement Results Data¶
- NMR
- https://www.etsi.org/deliver/etsi_ts/101500_101599/101503/08.27.00_60/ts_101503v082700p.pdf
- GSM API
- https://www.etsi.org/deliver/etsi_ts/101400_101499/101476/08.04.01_60/ts_101476v080401p.pdf
- UTRAN
- https://www.etsi.org/deliver/etsi_ts/125300_125399/125331/13.01.00_60/ts_125331v130100p.pdf
- E-UTRAN
- https://www.etsi.org/deliver/etsi_ts/136300_136399/136331/15.03.00_60/ts_136331v150300p.pdf
Single Linked List¶
- Btech Smart Class
- Data Structures Tutorials - Single Linked List with an example
- Visual Algo
- https://visualgo.net/en/list
What is Linked List¶
Like arrays, Linked List is a linear data structure. Unlike arrays, linked list elements are not stored at a contiguous location; the elements are linked using pointers. They include a series of connected nodes. Here, each node stores the data and the address of the next node.

Simply a list is a sequence of data, and the linked list is a sequence of data linked with each other.
The formal definition of a single linked list is as follows...
Single linked list is a sequence of elements in which every element has link to its next element in the sequence.
In any single linked list, the individual element is called as "Node". Every "Node" contains two fields, data field, and the next field. The data field is used to store actual value of the node and next field is used to store the address of next node in the sequence.
The graphical representation of a node in a single linked list is as follows...

Importent Points to be Remembered
In a single linked list, the address of the first node is always stored in a reference node known as "front" (Some times it is also known as "head").
Always next part (reference part) of the last node must be NULL.

Why Linked List?¶
- Arrays can be used to store linear data of similar types, but arrays have the following limitations:
- The size of the arrays is fixed:
- So we must know the upper limit on the number of elements in advance. Also, generally, the allocated memory is equal to the upper limit irrespective of the usage.
- Insertion of a new element / Deletion of a existing element in an array of elements is expensive:
- The room has to be created for the new elements and to create room existing elements have to be shifted but in Linked list if we have the head node then we can traverse to any node through it and insert new node at the required position.
Example:
- In a system, if we maintain a sorted list of IDs in an array id[] = [1000, 1010, 1050, 2000, 2040].
- If we want to insert a new ID 1005, then to maintain the sorted order, we have to move all the elements after 1000 (excluding 1000). - Deletion is also expensive with arrays until unless some special techniques are used. For example, to delete 1010 in id[], everything after 1010 has to be moved due to this so much work is being done which affects the efficiency of the code.
Advantages of Linked Lists over arrays:¶
- Dynamic Array.
- Ease of Insertion/Deletion.
Drawbacks of Linked Lists:¶
- Random access is not allowed. We have to access elements sequentially starting from the first node(head node). So we cannot do a binary search with linked lists efficiently with its default implementation.
- Extra memory space for a pointer is required with each element of the list.
- Not cache friendly. Since array elements are contiguous locations, there is locality of reference which is not there in case of linked lists.
Types of Linked Lists:¶
- Simple Linked List
- In this type of linked list, one can move or traverse the linked list in only one direction
- Doubly Linked List
- In this type of linked list, one can move or traverse the linked list in both directions (Forward and Backward)
- Circular Linked List
- In this type of linked list, the last node of the linked list contains the link of the first/head node of the linked list in its next pointer and the first/head node contains the link of the last node of the linked list in its prev pointer
Basic operations on Linked Lists¶
Setup Linked List¶
Before we implement actual operations, first we need to set up an empty list. First, perform the following steps before implementing actual operations.
- Step 1 - Include all the header files which are used in the program.
- Step 2 - Declare all the user defined functions.
- Step 3 - Define a Node structure with two members data and next
- Step 4 - Define a Node pointer 'head' and set it to NULL.
- Step 5 - Implement the main method by displaying operations menu and make suitable function calls in the main method to perform user selected operation.
Representation of Linked Lists¶
A linked list is represented by a pointer to the first node of the linked list. The first node is called the head of the linked list. If the linked list is empty, then the value of the head points to NULL.
Representation of Linked Lists¶
Each node in a list consists of at least two parts: - A Data Item (we can store integer, strings, or any type of data). - Pointer (Or Reference) to the next node (connects one node to another) or An address of another node
Representation of Linked Lists¶
- In C, we can represent a node using structures. Below is an example of a linked list node with integer data.
- In Java or C#, LinkedList can be represented as a class and a Node as a separate class. The LinkedList class contains a reference of Node class type.
Representation of Linked Lists - C / C++ Language¶
Representation of Linked Lists -C++ Language (Object based)¶
Representation of Linked Lists -Java Language¶
class LinkedList {
Node head; // head of the list
/* Linked list Node*/
class Node {
int data;
Node next;
// Constructor to create a new node
// Next is by default initialized
// as null
Node(int d)
{
data = d;
next = null;
}
}
}
Representation of Linked Lists -C# Language¶
class LinkedList {
// The first node(head) of the linked list
// Will be an object of type Node (null by default)
Node head;
class Node {
int data;
Node next;
// Constructor to create a new node
Node(int d) { data = d; }
}
}
Inserting At Beginning of the list¶
We can use the following steps to insert a new node at beginning of the single linked list...
- Step 1 - Create a
newNodewith given value. - Step 2 - Check whether list is Empty
(head == NULL) - Step 3 - If it is Empty then, set
newNode->next = NULLandhead = newNode. - Step 4 - If it is Not Empty then, set
newNode->next = headandhead = newNode
Inserting At End of the list¶
We can use the following steps to insert a new node at end of the single linked list...
- Step 1 - Create a newNode with given value and newNode → next as NULL.
- Step 2 - Check whether list is Empty (head == NULL).
- Step 3 - If it is Empty then, set head = newNode.
- Step 4 - If it is Not Empty then, define a node pointer temp and initialize with head.
- Step 5 - Keep moving the temp to its next node until it reaches to the last node in the list (until temp → next is equal to NULL).
- Step 6 - Set temp → next = newNode.
Inserting At Specific location in the list (After a Node)¶
We can use the following steps to insert a new node after a node in the single linked list...
- Step 1 - Create a newNode with given value.
- Step 2 - Check whether list is Empty (head == NULL)
- Step 3 - If it is Empty then, set newNode → next = NULL and head = newNode.
- Step 4 - If it is Not Empty then, define a node pointer temp and initialize with head.
Inserting At Specific location in the list (After a Node)¶
- Step 5 - Keep moving the temp to its next node until it reaches to the node after which we want to insert the newNode (until temp1 → data is equal to location, here location is the node value after which we want to insert the newNode).
- Step 6 - Every time check whether temp is reached to last node or not. If it is reached to last node then display 'Given node is not found in the list!!! Insertion not possible!!!' and terminate the function. Otherwise move the temp to next node.
- Step 7 - Finally, Set 'newNode → next = temp → next' and 'temp → next = newNode'
Construction of a simple linked list with 3 nodes - In C Language¶
// C program to implement a
// linked list
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
...
Construction of a simple linked list with 3 nodes - In C Language¶
...
// Driver's code
int main()
{
struct Node* head = NULL;
struct Node* second = NULL;
struct Node* third = NULL;
// allocate 3 nodes in the heap
head = (struct Node*)malloc(sizeof(struct Node));
second = (struct Node*)malloc(sizeof(struct Node));
third = (struct Node*)malloc(sizeof(struct Node));
/* Three blocks have been allocated dynamically.
We have pointers to these three blocks as head,
second and third
head second third
| | |
| | |
+---+-----+ +----+----+ +----+----+
| # | # | | # | # | | # | # |
+---+-----+ +----+----+ +----+----+
# represents any random value.
Data is random because we haven’t assigned
anything yet */
...
Construction of a simple linked list with 3 nodes - In C Language¶
head->data = 1; // assign data in first node
head->next = second; // Link first node with
// the second node
/* data has been assigned to the data part of the first
block (block pointed by the head). And next
pointer of first block points to second.
So they both are linked.
head second third
| | |
| | |
+---+---+ +----+----+ +-----+----+
| 1 | o----->| # | # | | # | # |
+---+---+ +----+----+ +-----+----+
*/
...
Construction of a simple linked list with 3 nodes - In C Language¶
// assign data to second node
second->data = 2;
// Link second node with the third node
second->next = third;
/* data has been assigned to the data part of the second
block (block pointed by second). And next
pointer of the second block points to the third
block. So all three blocks are linked.
head second third
| | |
| | |
+---+---+ +---+---+ +----+----+
| 1 | o----->| 2 | o-----> | # | # |
+---+---+ +---+---+ +----+----+ */
...
Construction of a simple linked list with 3 nodes - In C Language¶
third->data = 3; // assign data to third node
third->next = NULL;
/* data has been assigned to data part of third
block (block pointed by third). And next pointer
of the third block is made NULL to indicate
that the linked list is terminated here.
We have the linked list ready.
head
|
|
+---+---+ +---+---+ +----+------+
| 1 | o----->| 2 | o-----> | 3 | NULL |
+---+---+ +---+---+ +----+------+
Note that only head is sufficient to represent
the whole list. We can traverse the complete
list by following next pointers. */
return 0;
}
Construction of a simple linked list with 3 nodes - In C++¶
// C++ program to implement a
// linked list
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
};
...
Construction of a simple linked list with 3 nodes - In C++¶
// Driver's code
int main()
{
Node* head = NULL;
Node* second = NULL;
Node* third = NULL;
// allocate 3 nodes in the heap
head = new Node();
second = new Node();
third = new Node();
/* Three blocks have been allocated dynamically.
We have pointers to these three blocks as head,
second and third
head second third
| | |
| | |
+---+-----+ +----+----+ +----+----+
| # | # | | # | # | | # | # |
+---+-----+ +----+----+ +----+----+
# represents any random value.
Data is random because we haven’t assigned
anything yet */
...
Construction of a simple linked list with 3 nodes - In C++¶
head->data = 1; // assign data in first node
head->next = second; // Link first node with
// the second node
/* data has been assigned to the data part of first
block (block pointed by the head). And next
pointer of the first block points to second.
So they both are linked.
head second third
| | |
| | |
+---+---+ +----+----+ +-----+----+
| 1 | o----->| # | # | | # | # |
+---+---+ +----+----+ +-----+----+
*/
...
Construction of a simple linked list with 3 nodes - In C++¶
// assign data to second node
second->data = 2;
// Link second node with the third node
second->next = third;
/* data has been assigned to the data part of the second
block (block pointed by second). And next
pointer of the second block points to the third
block. So all three blocks are linked.
head second third
| | |
| | |
+---+---+ +---+---+ +----+----+
| 1 | o----->| 2 | o-----> | # | # |
+---+---+ +---+---+ +----+----+ */
...
Construction of a simple linked list with 3 nodes - In C++¶
third->data = 3; // assign data to third node
third->next = NULL;
/* data has been assigned to the data part of the third
block (block pointed by third). And next pointer
of the third block is made NULL to indicate
that the linked list is terminated here.
We have the linked list ready.
head
|
|
+---+---+ +---+---+ +----+------+
| 1 | o----->| 2 | o-----> | 3 | NULL |
+---+---+ +---+---+ +----+------+
Note that only the head is sufficient to represent
the whole list. We can traverse the complete
list by following the next pointers. */
return 0;
}
// This code is contributed by rathbhupendra
Construction of a simple linked list with 3 nodes in Java¶
// A simple Java program to introduce a linked list
class LinkedList {
Node head; // head of list
/* Linked list Node. This inner class is made static so
that main() can access it */
static class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
} // Constructor
}
...
Construction of a simple linked list with 3 nodes in Java¶
/* method to create a simple linked list with 3 nodes*/
public static void main(String[] args)
{
/* Start with the empty list. */
LinkedList llist = new LinkedList();
llist.head = new Node(1);
Node second = new Node(2);
Node third = new Node(3);
/* Three nodes have been allocated dynamically.
We have references to these three blocks as head,
second and third
llist.head second third
| | |
| | |
+----+------+ +----+------+ +----+------+
| 1 | null | | 2 | null | | 3 | null |
+----+------+ +----+------+ +----+------+
*/
...
Construction of a simple linked list with 3 nodes in Java¶
llist.head.next = second; // Link first node with
// the second node
/* Now next of the first Node refers to the second.
So they both are linked.
llist.head second third
| | |
| | |
+----+------+ +----+------+ +----+------+
| 1 | o-------->| 2 | null | | 3 | null |
+----+------+ +----+------+ +----+------+ */
...
Construction of a simple linked list with 3 nodes in Java¶
second.next
= third; // Link second node with the third node
/* Now next of the second Node refers to third. So
all three nodes are linked.
llist.head second third
| | |
| | |
+----+------+ +----+------+ +----+------+
| 1 | o-------->| 2 | o-------->| 3 | null |
+----+------+ +----+------+ +----+------+ */
}
}
Construction of a simple linked list with 3 nodes in C¶
// A simple C# program to introduce a linked list
using System;
public class LinkedList {
Node head; // head of list
/* Linked list Node. This inner class is made static so
that main() can access it */
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
} // Constructor
}
...
Construction of a simple linked list with 3 nodes in C¶
/* method to create a simple linked list with 3 nodes*/
public static void Main(String[] args)
{
/* Start with the empty list. */
LinkedList llist = new LinkedList();
llist.head = new Node(1);
Node second = new Node(2);
Node third = new Node(3);
/* Three nodes have been allocated dynamically.
We have references to these three blocks as head,
second and third
llist.head second third
| | |
| | |
+----+------+ +----+------+ +----+------+
| 1 | null | | 2 | null | | 3 | null |
+----+------+ +----+------+ +----+------+ */
...
Construction of a simple linked list with 3 nodes in C¶
llist.head.next = second; // Link first node with
// the second node
/* Now next of first Node refers to second. So they
both are linked.
llist.head second third
| | |
| | |
+----+------+ +----+------+ +----+------+
| 1 | o-------->| 2 | null | | 3 | null |
+----+------+ +----+------+ +----+------+ */
...
Construction of a simple linked list with 3 nodes in C¶
second.next
= third; // Link second node with the third node
/* Now next of the second Node refers to third. So
all three nodes are linked.
llist.head second third
| | |
| | |
+----+------+ +----+------+ +----+------+
| 1 | o-------->| 2 | o-------->| 3 | null |
+----+------+ +----+------+ +----+------+ */
}
}
// This code has been contributed by 29AjayKumar
Linked List Deletion¶
In a single linked list, the deletion operation can be performed in three ways. They are as follows...
- Deleting from Beginning of the list
- Deleting from End of the list
- Deleting a Specific Node
Deleting from Beginning of the list¶
We can use the following steps to delete a node from beginning of the single linked list...
- Step 1 - Check whether list is Empty (head == NULL)
- Step 2 - If it is Empty then, display 'List is Empty!!! Deletion is not possible' and terminate the function.
- Step 3 - If it is Not Empty then, define a Node pointer 'temp' and initialize with head.
- Step 4 - Check whether list is having only one node (temp → next == NULL)
- Step 5 - If it is TRUE then set head = NULL and delete temp (Setting Empty list conditions)
- Step 6 - If it is FALSE then set head = temp → next, and delete temp.
Deleting from End of the list¶
We can use the following steps to delete a node from end of the single linked list...
- Step 1 - Check whether list is Empty (head == NULL)
- Step 2 - If it is Empty then, display 'List is Empty!!! Deletion is not possible' and terminate the function.
- Step 3 - If it is Not Empty then, define two Node pointers 'temp1' and 'temp2' and initialize 'temp1' with head.
Deleting from End of the list¶
- Step 4 - Check whether list has only one Node (temp1 → next == NULL)
- Step 5 - If it is TRUE. Then, set head = NULL and delete temp1. And terminate the function. (Setting Empty list condition)
- Step 6 - If it is FALSE. Then, set 'temp2 = temp1 ' and move temp1 to its next node. Repeat the same until it reaches to the last node in the list. (until temp1 → next == NULL)
- Step 7 - Finally, Set temp2 → next = NULL and delete temp1.
Deleting a Specific Node from the list¶
We can use the following steps to delete a specific node from the single linked list...
- Step 1 - Check whether list is Empty (head == NULL)
- Step 2 - If it is Empty then, display 'List is Empty!!! Deletion is not possible' and terminate the function.
- Step 3 - If it is Not Empty then, define two Node pointers 'temp1' and 'temp2' and initialize 'temp1' with head.
Deleting a Specific Node from the list¶
- Step 4 - Keep moving the temp1 until it reaches to the exact node to be deleted or to the last node. And every time set 'temp2 = temp1' before moving the 'temp1' to its next node.
- Step 5 - If it is reached to the last node then display 'Given node not found in the list! Deletion not possible!!!'. And terminate the function.
- Step 6 - If it is reached to the exact node which we want to delete, then check whether list is having only one node or not
Deleting a Specific Node from the list¶
- Step 7 - If list has only one node and that is the node to be deleted, then set head = NULL and delete temp1 (free(temp1)).
- Step 8 - If list contains multiple nodes, then check whether temp1 is the first node in the list (temp1 == head).
- Step 9 - If temp1 is the first node then move the head to the next node (head = head → next) and delete temp1.
Deleting a Specific Node from the list¶
- Step 10 - If temp1 is not first node then check whether it is last node in the list (temp1 → next == NULL).
- Step 11 - If temp1 is last node then set temp2 → next = NULL and delete temp1 (free(temp1)).
- Step 12 - If temp1 is not first node and not last node then set temp2 → next = temp1 → next and delete temp1 (free(temp1)).
Displaying a Single Linked List¶
We can use the following steps to display the elements of a single linked list...
- Step 1 - Check whether list is Empty (head == NULL)
- Step 2 - If it is Empty then, display 'List is Empty!!!' and terminate the function.
- Step 3 - If it is Not Empty then, define a Node pointer 'temp' and initialize with head.
- Step 4 - Keep displaying temp → data with an arrow (--->) until temp reaches to the last node
- Step 5 - Finally display temp → data with arrow pointing to NULL (temp → data ---> NULL).
Traversal of a Linked List¶
In the previous program, we created a simple linked list with three nodes. Let us traverse the created list and print the data of each node. For traversal, let us write a general-purpose function printList() that prints any given list.
Traversal of a Linked List - C¶
// A simple C program for
// traversal of a linked list
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
...
Traversal of a Linked List - C¶
// This function prints contents of linked list starting
// from the given node
void printList(struct Node* n)
{
while (n != NULL) {
printf(" %d ", n->data);
n = n->next;
}
}
...
Traversal of a Linked List - C¶
// Driver's code
int main()
{
struct Node* head = NULL;
struct Node* second = NULL;
struct Node* third = NULL;
// allocate 3 nodes in the heap
head = (struct Node*)malloc(sizeof(struct Node));
second = (struct Node*)malloc(sizeof(struct Node));
third = (struct Node*)malloc(sizeof(struct Node));
...
Traversal of a Linked List - C¶
head->data = 1; // assign data in first node
head->next = second; // Link first node with second
second->data = 2; // assign data to second node
second->next = third;
third->data = 3; // assign data to third node
third->next = NULL;
// Function call
printList(head);
return 0;
}
Traversal of a Linked List - C++¶
// A simple C++ program for
// traversal of a linked list
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
};
...
Traversal of a Linked List - C++¶
// This function prints contents of linked list
// starting from the given node
void printList(Node* n)
{
while (n != NULL) {
cout << n->data << " ";
n = n->next;
}
}
...
Traversal of a Linked List - C++¶
// Driver's code
int main()
{
Node* head = NULL;
Node* second = NULL;
Node* third = NULL;
// allocate 3 nodes in the heap
head = new Node();
second = new Node();
third = new Node();
...
Traversal of a Linked List - C++¶
head->data = 1; // assign data in first node
head->next = second; // Link first node with second
second->data = 2; // assign data to second node
second->next = third;
third->data = 3; // assign data to third node
third->next = NULL;
// Function call
printList(head);
return 0;
}
// This is code is contributed by rathbhupendra
Traversal of a Linked List - Java¶
// A simple Java program for traversal of a linked list
class LinkedList {
Node head; // head of list
/* Linked list Node. This inner class is made static so
that main() can access it */
static class Node {
int data;
Node next;
Node(int d)
{
this.data = d;
next = null;
} // Constructor
}
...
Traversal of a Linked List - Java¶
/* This function prints contents of linked list starting
* from head */
public void printList()
{
Node n = head;
while (n != null) {
System.out.print(n.data + " ");
n = n.next;
}
}
...
Traversal of a Linked List - Java¶
// Driver's code
public static void main(String[] args)
{
/* Start with the empty list. */
LinkedList llist = new LinkedList();
llist.head = new Node(1);
Node second = new Node(2);
Node third = new Node(3);
...
Traversal of a Linked List - Java¶
llist.head.next = second; // Link first node with
// the second node
second.next
= third; // Link second node with the third node
// Function call
llist.printList();
}
}
Traversal of a Linked List - C¶
// C# program for traversal of a linked list
using System;
public class LinkedList {
Node head; // head of list
/* Linked list Node. This inner
class is made static so that
main() can access it */
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
} // Constructor
}
...
Traversal of a Linked List - C¶
/* This function prints contents of
linked list starting from head */
public void printList()
{
Node n = head;
while (n != null) {
Console.Write(n.data + " ");
n = n.next;
}
}
...
Traversal of a Linked List - C¶
// Driver's code
public static void Main(String[] args)
{
/* Start with the empty list. */
LinkedList llist = new LinkedList();
llist.head = new Node(1);
Node second = new Node(2);
Node third = new Node(3);
llist.head.next = second; // Link first node with
// the second node
second.next
= third; // Link second node with the third node
// Function call
llist.printList();
}
}
/* This code contributed by PrinciRaj1992 */
Output¶
Time Complexity¶
| Time Complexity | Worst Case | Average Case |
|---|---|---|
| Search | O(n) | O(n) |
| Insert at Start | O(1) | O(1) |
| Deletion from Start | O(1) | O(1) |
Auxiliary Space: O(N)
Complete C Example of Single Linked List¶
// SingleLinkedList.c : This file contains the 'main' function. Program execution begins and ends there.
//
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#define clrscr(); system("cls");
...
Complete C Example of Single Linked List¶
void insertAtBeginning(int);
void insertAtEnd(int);
void insertBetween(int, int, int);
void display();
void removeBeginning();
void removeEnd();
void removeSpecific(int);
...
Complete C Example of Single Linked List¶
Complete C Example of Single Linked List¶
void main()
{
int choice, value, choice1, loc1, loc2;
clrscr();
while (1) {
printf("\n\n****** MENU ******\n\n");
printf("1. Insert\n");
printf("2. Display\n");
printf("3. Delete\n");
printf("4. Exit\n");
printf("Enter your choice : ");
scanf("%d", &choice);
...
Complete C Example of Single Linked List¶
switch (choice)
{
case 1: printf("Enter the value to be insert: ");
scanf("%d", &value);
while (1) {
printf("Where you want to insert: \n");
printf("1. At Beginning\n");
printf("2. At End\n");
printf("3. Between\n");
printf("Enter your choice: ");
scanf("%d", &choice1);
switch (choice1)
{
case 1:
insertAtBeginning(value);
break;
case 2:
insertAtEnd(value);
break;
case 3:
printf("Enter the two values where you want to insert: ");
scanf("%d%d", &loc1, &loc2);
insertBetween(value, loc1, loc2);
break;
default:
printf("\nWrong Input!! Try again!!!\n\n");
continue;
}
break;
}
break;
...
Complete C Example of Single Linked List¶
Complete C Example of Single Linked List¶
case 3:
printf("How do you want to Delete: \n");
printf("1. From Beginning\n");
printf("2. From End\n");
printf("3. Spesific\n");
printf("Enter your choice: ");
scanf("%d", &choice1);
switch (choice1){
case 1:
removeBeginning();
break;
case 2:
removeEnd();
break;
case 3:
printf("Enter the value which you wanto delete: ");
scanf("%d", &loc2);
removeSpecific(loc2);
break;
default:
printf("\nWrong Input!! Try again!!!\n\n");
break;
}
break;
...
Complete C Example of Single Linked List¶
Complete C Example of Single Linked List¶
void insertAtBeginning(int value)
{
struct Node* newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
if (head == NULL)
{
newNode->next = NULL;
head = newNode;
}
else
{
newNode->next = head;
head = newNode;
}
printf("\nOne node inserted!!!\n");
}
...
Complete C Example of Single Linked List¶
void insertAtEnd(int value)
{
struct Node* newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
newNode->next = NULL;
if (head == NULL)
head = newNode;
else
{
struct Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
temp->next = newNode;
}
printf("\nOne node inserted!!!\n");
}
...
Complete C Example of Single Linked List¶
void insertBetween(int value, int loc1, int loc2)
{
struct Node* newNode;
newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
if (head == NULL){
newNode->next = NULL;
head = newNode;
}else{
struct Node* temp = head;
while (temp->data != loc1 && temp->data != loc2)
temp = temp->next;
newNode->next = temp->next;
temp->next = newNode;
}
printf("\nOne node inserted!!!\n");
}
...
Complete C Example of Single Linked List¶
void removeBeginning()
{
if (head == NULL)
printf("\n\nList is Empty!!!");
else
{
struct Node* temp = head;
if (head->next == NULL)
{
head = NULL;
free(temp);
}
else
{
head = temp->next;
free(temp);
printf("\nOne node deleted!!!\n\n");
}
}
}
...
Complete C Example of Single Linked List¶
void removeEnd()
{
if (head == NULL)
{
printf("\nList is Empty!!!\n");
}
else
{
struct Node* temp1 = head, * temp2 = 0;
if (head->next == NULL)
head = NULL;
else
{
while (temp1->next != NULL)
{
temp2 = temp1;
temp1 = temp1->next;
}
temp2->next = NULL;
}
free(temp1);
printf("\nOne node deleted!!!\n\n");
}
}
...
Complete C Example of Single Linked List¶
void removeSpecific(int delValue)
{
struct Node* temp1 = head, * temp2 = 0;
while (temp1->data != delValue)
{
if (temp1->next == NULL) {
printf("\nGiven node not found in the list!!!");
return;
}
temp2 = temp1;
temp1 = temp1->next;
}
temp2->next = temp1->next;
free(temp1);
printf("\nOne node deleted!!!\n\n");
}
...
Complete C Example of Single Linked List¶
void display()
{
if (head == NULL)
{
printf("\nList is Empty\n");
}
else
{
struct Node* temp = head;
printf("\n\nList elements are - \n");
while (temp->next != NULL)
{
printf("%d --->", temp->data);
temp = temp->next;
}
printf("%d --->NULL", temp->data);
}
}
References¶
What is Linked List - GeeksforGeeks
Circular Linked List¶
- Btech Smart Class
- Data Structures Tutorials - Circular Linked List with an example | Implementation
- Geeks for Geeks
- Circular Linked List | Set 1 (Introduction and Applications) - GeeksforGeeks
- Geeks for Geeks
- Circular Linked List | Set 2 (Traversal) - GeeksforGeeks
Circular Linked List¶
-
In this article, you will learn what circular linked list is and its types with implementation.
-
A circular linked list is a type of linked list in which the first and the last nodes are also connected to each other to form a circle.
-
There are basically two types of circular linked list:
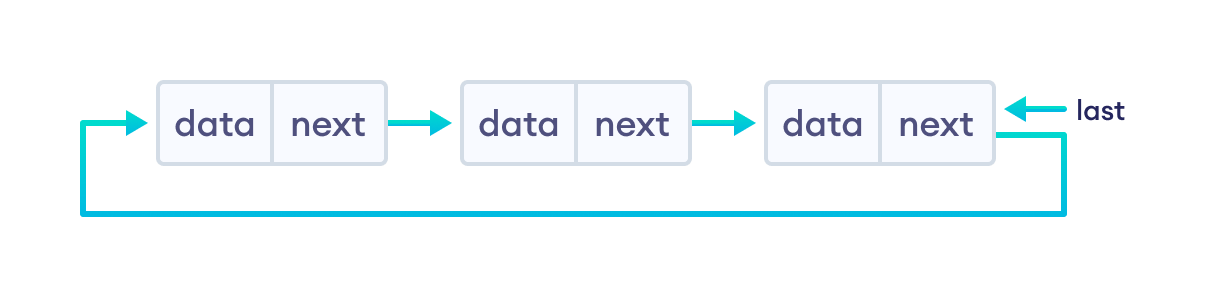
1. Circular Singly Linked List¶
- Here, the address of the last node consists of the address of the first node.
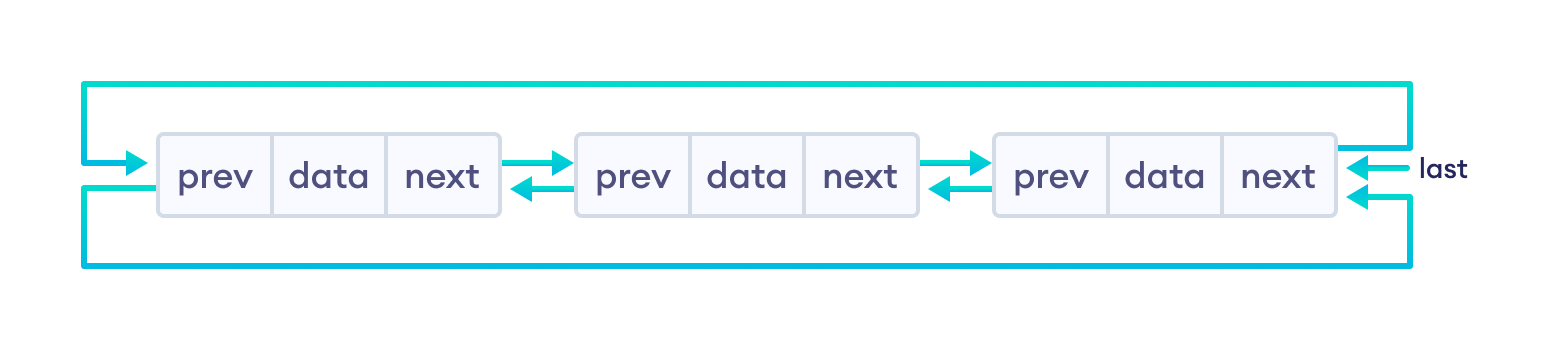
2. Circular Doubly Linked List¶
Here, in addition to the last node storing the address of the first node, the first node will also store the address of the last node.
Note: We will be using the singly circular linked list to represent the working of circular linked list.
Representation of Circular Linked List¶
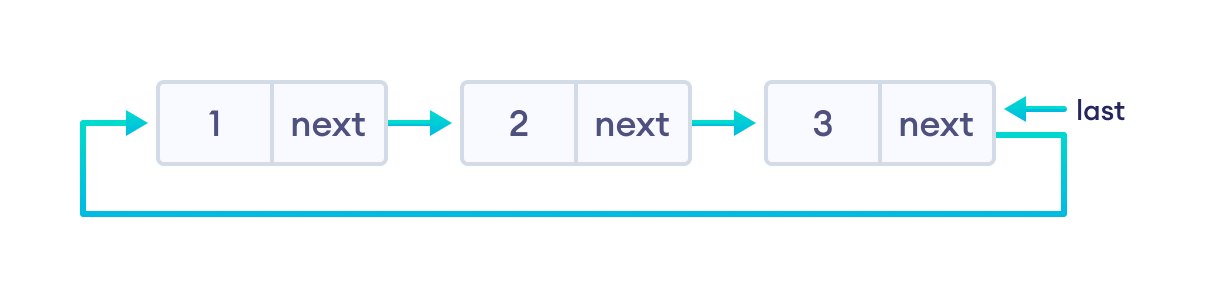
Let's see how we can represent a circular linked list on an algorithm/code. Suppose we have a linked list:
Representation of Circular Linked List¶
Here, the single node is represented as
Representation of Circular Linked List¶
Each struct node has a data item and a pointer to the next struct node.
Now we will create a simple circular linked list with three items to understand how this works.
Representation of Circular Linked List¶
/* Initialize nodes */
struct node *last;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;
/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));
...
Representation of Circular Linked List¶
/* Assign data values */
one->data = 1;
two->data = 2;
three->data = 3;
/* Connect nodes */
one->next = two;
two->next = three;
three->next = one;
/* Save address of third node in last */
last = three;
Representation of Circular Linked List¶
In the above code, one, two, and three are the nodes with data items 1, 2, and 3 respectively.
- For node one
- next stores the address of two (there is no node before it)
- For node two
- next stores the address of three
- For node three
- next stores
NULL(there is no node after it) - next points to node one
- next stores
Insertion on a Circular Linked List¶
-
We can insert elements at 3 different positions of a circular linked list:
- Insertion in-between nodes
- Insertion at the end
Insertion on a Circular Linked List¶
- Suppose we have a circular linked list with elements 1, 2, and 3.

Insertion on a Circular Linked List¶
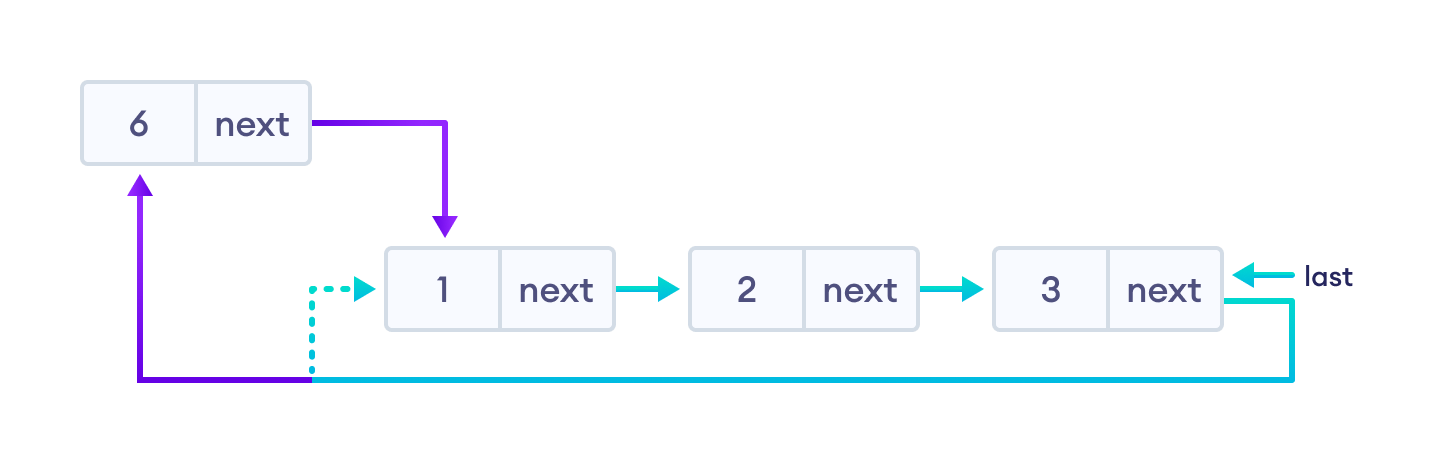
Let's add a node with value 6 at different positions of the circular linked list we made above. The first step is to create a new node.
- allocate memory for
newNode - assign the data to
newNode

1. Insertion at the Beginning¶
- store the address of the current first node in the
newNode(i.e. pointing thenewNodeto the current first node) - point the last node to
newNode(i.e makingnewNodeas head)
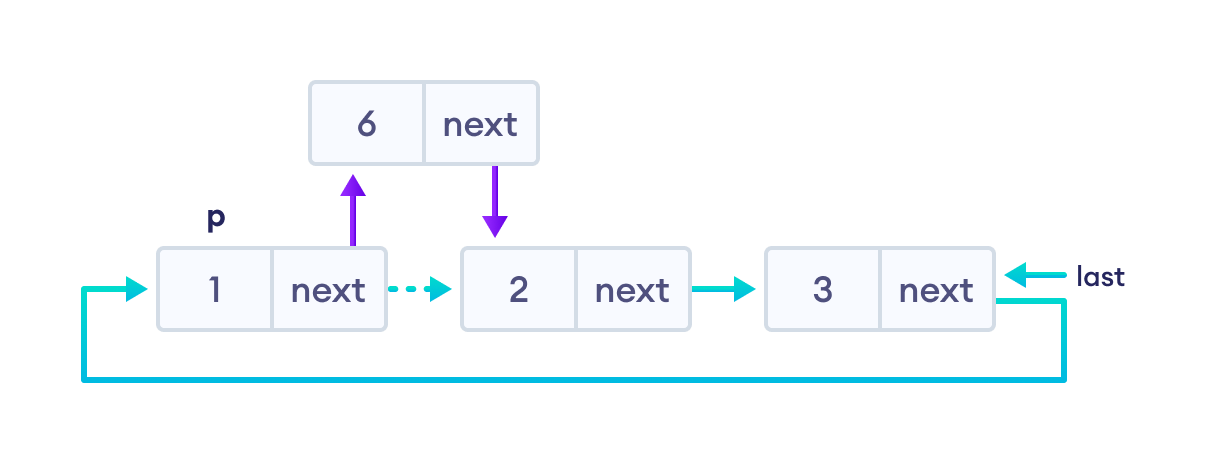
2. Insertion in between two nodes¶
- Let's insert newNode after the first node.
- travel to the node given (let this node be
p) - point the
nextofnewNodeto the node next top - store the address of
newNodeatnextofp
- travel to the node given (let this node be
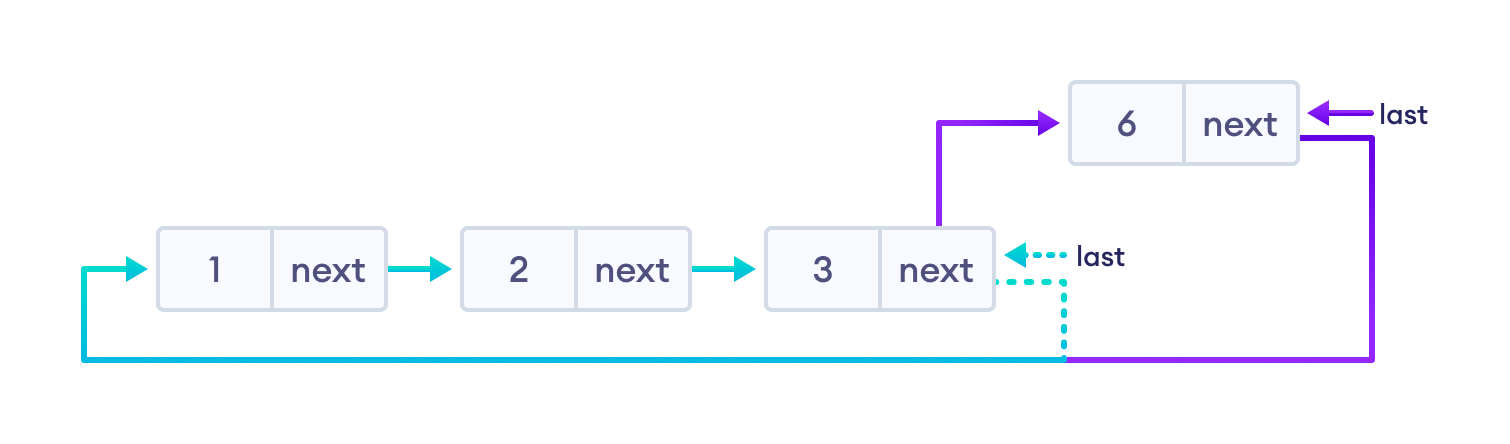
3. Insertion at the end¶
- store the address of the head node to
nextof newNode (makingnewNodethe last node) - point the current last node to
newNode - make
newNodeas the last node
Deletion on a Circular Linked List¶
Suppose we have a double-linked list with elements 1, 2, and 3.

Deletion on a Circular Linked List¶
- If the node to be deleted is the only node
- free the memory occupied by the node
- store NULL in
last
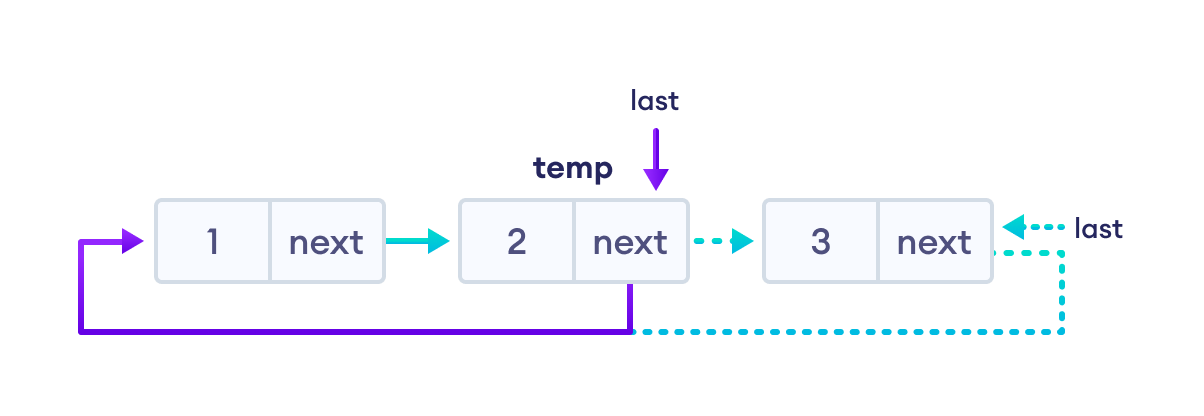
- If last node is to be deleted
- find the node before the last node (let it be
temp) - store the address of the node next to the last node in
temp - free the memory of last
- make
tempas the last node
- find the node before the last node (let it be
Deletion on a Circular Linked List¶
Deletion on a Circular Linked List¶
-
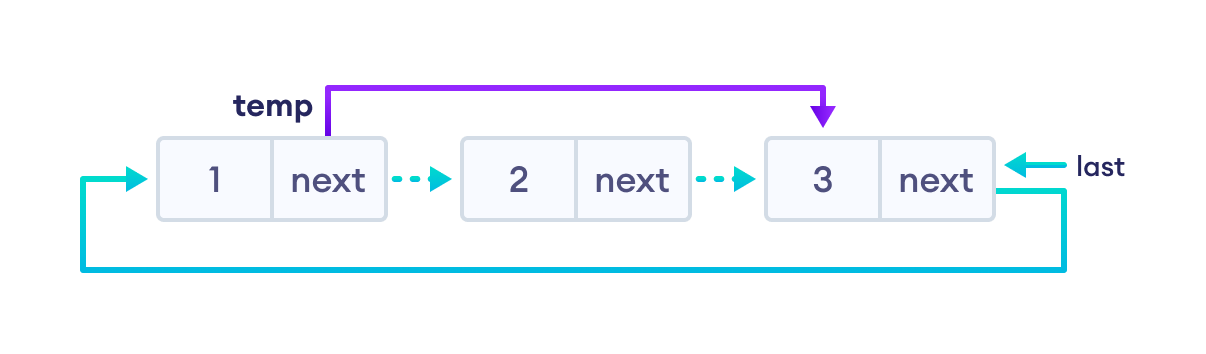
- If any other nodes are to be deleted
- travel to the node to be deleted (here we are deleting node 2)
- let the node before node 2 be
temp - store the address of the node next to 2 in
temp - free the memory of 2
Deletion on a Circular Linked List¶
Circular Linked List Code in C¶
// C code to perform circular linked list operations
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
¶
// C code to perform circular linked list operations
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
Circular Linked List Code in C¶
struct Node* addToEmpty(struct Node* last, int data) {
if (last != NULL) return last;
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// assign data to the new node
newNode->data = data;
// assign last to newNode
last = newNode;
// create link to iteself
last->next = last;
return last;
}
¶
struct Node* addToEmpty(struct Node* last, int data) {
if (last != NULL) return last;
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// assign data to the new node
newNode->data = data;
// assign last to newNode
last = newNode;
// create link to iteself
last->next = last;
return last;
}
Circular Linked List Code in C¶
// add node to the front
struct Node* addFront(struct Node* last, int data) {
// check if the list is empty
if (last == NULL) return addToEmpty(last, data);
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// store the address of the current first node in the newNode
newNode->next = last->next;
// make newNode as head
last->next = newNode;
return last;
}
¶
// add node to the front
struct Node* addFront(struct Node* last, int data) {
// check if the list is empty
if (last == NULL) return addToEmpty(last, data);
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// store the address of the current first node in the newNode
newNode->next = last->next;
// make newNode as head
last->next = newNode;
return last;
}
Circular Linked List Code in C¶
// add node to the end
struct Node* addEnd(struct Node* last, int data) {
// check if the node is empty
if (last == NULL) return addToEmpty(last, data);
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// store the address of the head node to next of newNode
newNode->next = last->next;
// point the current last node to the newNode
last->next = newNode;
// make newNode as the last node
last = newNode;
return last;
}
¶
// add node to the end
struct Node* addEnd(struct Node* last, int data) {
// check if the node is empty
if (last == NULL) return addToEmpty(last, data);
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// store the address of the head node to next of newNode
newNode->next = last->next;
// point the current last node to the newNode
last->next = newNode;
// make newNode as the last node
last = newNode;
return last;
}
Circular Linked List Code in C¶
// insert node after a specific node
struct Node* addAfter(struct Node* last, int data, int item) {
// check if the list is empty
if (last == NULL) return NULL;
struct Node *newNode, *p;
p = last->next;
do {
// if the item is found, place newNode after it
if (p->data == item) {
// allocate memory to the new node
newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// make the next of the current node as the next of newNode
newNode->next = p->next;
// put newNode to the next of p
p->next = newNode;
// if p is the last node, make newNode as the last node
if (p == last) last = newNode;
return last;
}
p = p->next;
} while (p != last->next);
printf("\nThe given node is not present in the list");
return last;
}
¶
// insert node after a specific node
struct Node* addAfter(struct Node* last, int data, int item) {
// check if the list is empty
if (last == NULL) return NULL;
struct Node *newNode, *p;
p = last->next;
do {
// if the item is found, place newNode after it
if (p->data == item) {
// allocate memory to the new node
newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// make the next of the current node as the next of newNode
newNode->next = p->next;
// put newNode to the next of p
p->next = newNode;
// if p is the last node, make newNode as the last node
if (p == last) last = newNode;
return last;
}
p = p->next;
} while (p != last->next);
printf("\nThe given node is not present in the list");
return last;
}
Circular Linked List Code in C¶
// delete a node
void deleteNode(struct Node** last, int key) {
// if linked list is empty
if (*last == NULL) return;
// if the list contains only a single node
if ((*last)->data == key && (*last)->next == *last) {
free(*last);
*last = NULL;
return;
}
struct Node *temp = *last, *d;
// if last is to be deleted
if ((*last)->data == key) {
// find the node before the last node
while (temp->next != *last) temp = temp->next;
// point temp node to the next of last i.e. first node
temp->next = (*last)->next;
free(*last);
*last = temp->next;
}
// travel to the node to be deleted
while (temp->next != *last && temp->next->data != key) {
temp = temp->next;
}
// if node to be deleted was found
if (temp->next->data == key) {
d = temp->next;
temp->next = d->next;
free(d);
}
}
¶
// delete a node
void deleteNode(struct Node** last, int key) {
// if linked list is empty
if (*last == NULL) return;
// if the list contains only a single node
if ((*last)->data == key && (*last)->next == *last) {
free(*last);
*last = NULL;
return;
}
struct Node *temp = *last, *d;
// if last is to be deleted
if ((*last)->data == key) {
// find the node before the last node
while (temp->next != *last) temp = temp->next;
// point temp node to the next of last i.e. first node
temp->next = (*last)->next;
free(*last);
*last = temp->next;
}
// travel to the node to be deleted
while (temp->next != *last && temp->next->data != key) {
temp = temp->next;
}
// if node to be deleted was found
if (temp->next->data == key) {
d = temp->next;
temp->next = d->next;
free(d);
}
}
Circular Linked List Code in C¶
void traverse(struct Node* last) {
struct Node* p;
if (last == NULL) {
printf("The list is empty");
return;
}
p = last->next;
do {
printf("%d ", p->data);
p = p->next;
} while (p != last->next);
}
¶
void traverse(struct Node* last) {
struct Node* p;
if (last == NULL) {
printf("The list is empty");
return;
}
p = last->next;
do {
printf("%d ", p->data);
p = p->next;
} while (p != last->next);
}
Circular Linked List Code in C¶
int main() {
struct Node* last = NULL;
last = addToEmpty(last, 6);
last = addEnd(last, 8);
last = addFront(last, 2);
last = addAfter(last, 10, 2);
traverse(last);
deleteNode(&last, 8);
printf("\n");
traverse(last);
return 0;
}
Circular Linked List Code in C++¶
// C++ code to perform circular linked list operations
#include <iostream>
using namespace std;
struct Node {
int data;
struct Node* next;
};
Circular Linked List Code in C++¶
struct Node* addToEmpty(struct Node* last, int data) {
if (last != NULL) return last;
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// assign data to the new node
newNode->data = data;
// assign last to newNode
last = newNode;
// create link to iteself
last->next = last;
return last;
}
Circular Linked List Code in C++¶
// add node to the front
struct Node* addFront(struct Node* last, int data) {
// check if the list is empty
if (last == NULL) return addToEmpty(last, data);
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// store the address of the current first node in the newNode
newNode->next = last->next;
// make newNode as head
last->next = newNode;
return last;
}
Circular Linked List Code in C++¶
// add node to the end
struct Node* addEnd(struct Node* last, int data) {
// check if the node is empty
if (last == NULL) return addToEmpty(last, data);
// allocate memory to the new node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// store the address of the head node to next of newNode
newNode->next = last->next;
// point the current last node to the newNode
last->next = newNode;
// make newNode as the last node
last = newNode;
return last;
}
Circular Linked List Code in C++¶
// insert node after a specific node
struct Node* addAfter(struct Node* last, int data, int item) {
// check if the list is empty
if (last == NULL) return NULL;
struct Node *newNode, *p;
p = last->next;
do {
// if the item is found, place newNode after it
if (p->data == item) {
// allocate memory to the new node
newNode = (struct Node*)malloc(sizeof(struct Node));
// add data to the node
newNode->data = data;
// make the next of the current node as the next of newNode
newNode->next = p->next;
// put newNode to the next of p
p->next = newNode;
// if p is the last node, make newNode as the last node
if (p == last) last = newNode;
return last;
}
p = p->next;
} while (p != last->next);
cout << "\nThe given node is not present in the list" << endl;
return last;
}
Circular Linked List Code in C++¶
// delete a node
void deleteNode(Node** last, int key) {
// if linked list is empty
if (*last == NULL) return;
// if the list contains only a single node
if ((*last)->data == key && (*last)->next == *last) {
free(*last);
*last = NULL;
return;
}
Node *temp = *last, *d;
// if last is to be deleted
if ((*last)->data == key) {
// find the node before the last node
while (temp->next != *last) temp = temp->next;
// point temp node to the next of last i.e. first node
temp->next = (*last)->next;
free(*last);
*last = temp->next;
}
// travel to the node to be deleted
while (temp->next != *last && temp->next->data != key) {
temp = temp->next;
}
// if node to be deleted was found
if (temp->next->data == key) {
d = temp->next;
temp->next = d->next;
free(d);
}
}
Circular Linked List Code in C++¶
void traverse(struct Node* last) {
struct Node* p;
if (last == NULL) {
cout << "The list is empty" << endl;
return;
}
p = last->next;
do {
cout << p->data << " ";
p = p->next;
} while (p != last->next);
}
Circular Linked List Code in C++¶
int main() {
struct Node* last = NULL;
last = addToEmpty(last, 6);
last = addEnd(last, 8);
last = addFront(last, 2);
last = addAfter(last, 10, 2);
traverse(last);
deleteNode(&last, 8);
cout << endl;
traverse(last);
return 0;
}
Circular Linked List Code in Java¶
// Java code to perform circular linked list operations
class CircularLinkedList {
static class Node {
int data;
Node next;
};
...
```
---
### Circular Linked List Code in Java
``` java
static Node addToEmpty(Node last, int data) {
if (last != null)
return last;
// allocate memory to the new node
Node newNode = new Node();
// assign data to the new node
newNode.data = data;
// assign last to newNode
last = newNode;
// create link to iteself
newNode.next = last;
return last;
}
...
```
---
### Circular Linked List Code in Java
``` java
// add node to the front
static Node addFront(Node last, int data) {
if (last == null)
return addToEmpty(last, data);
// allocate memory to the new node
Node newNode = new Node();
// add data to the node
newNode.data = data;
// store the address of the current first node in the newNode
newNode.next = last.next;
// make newNode as head
last.next = newNode;
return last;
}
...
```
---
### Circular Linked List Code in Java
``` java
// add node to the end
static Node addEnd(Node last, int data) {
if (last == null)
return addToEmpty(last, data);
// allocate memory to the new node
Node newNode = new Node();
// add data to the node
newNode.data = data;
// store the address of the head node to next of newNode
newNode.next = last.next;
// point the current last node to the newNode
last.next = newNode;
// make newNode as the last node
last = newNode;
return last;
}
...
```
---
### Circular Linked List Code in Java
``` java
static Node addAfter(Node last, int data, int item) {
if (last == null)
return null;
Node newNode, p;
p = last.next;
do {
// if the item is found, place newNode after it
if (p.data == item) {
// allocate memory to the new node
newNode = new Node();
// add data to the node
newNode.data = data;
// make the next of the current node as the next of newNode
newNode.next = p.next;
// put newNode to the next of p
p.next = newNode;
// if p is the last node, make newNode as the last node
if (p == last)
last = newNode;
return last;
}
p = p.next;
} while (p != last.next);
System.out.println(item + "The given node is not present in the list");
return last;
}
...
```
---
### Circular Linked List Code in Java
``` java
// delete a node
static Node deleteNode(Node last, int key) {
// if linked list is empty
if (last == null)
return null;
// if the list contains only a single node
if (last.data == key && last.next == last) {
last = null;
return last;
}
Node temp = last, d = new Node();
// if last is to be deleted
if (last.data == key) {
// find the node before the last node
while (temp.next != last) {
temp = temp.next;
}
// point temp node to the next of last i.e. first node
temp.next = last.next;
last = temp.next;
}
// travel to the node to be deleted
while (temp.next != last && temp.next.data != key) {
temp = temp.next;
}
// if node to be deleted was found
if (temp.next.data == key) {
d = temp.next;
temp.next = d.next;
}
return last;
}
...
```
---
### Circular Linked List Code in Java
``` java
static void traverse(Node last) {
Node p;
if (last == null) {
System.out.println("List is empty.");
return;
}
p = last.next;
do {
System.out.print(p.data + " ");
p = p.next;
}
while (p != last.next);
}
...
```
---
### Circular Linked List Code in Java
``` java
public static void main(String[] args) {
Node last = null;
last = addToEmpty(last, 6);
last = addEnd(last, 8);
last = addFront(last, 2);
last = addAfter(last, 10, 2);
traverse(last);
deleteNode(last, 8);
traverse(last);
}
}
Circular Linked List Complexity¶
| Circular Linked List Complexity | Time Complexity | Space Complexity |
|---|---|---|
| Insertion Operation | O(1) or O(n) | O(1) |
| Deletion Operation | O(1) | O(1) |
Circular Linked List Complexity¶
-
- Complexity of Insertion Operation**
- The insertion operations that do not require traversal have the time complexity of
O(1). - And, an insertion that requires traversal has a time complexity of
O(n). - The space complexity is
O(1).
-
- Complexity of Deletion Operation**
- All deletion operations run with a time complexity of
O(1). - And, the space complexity is
O(1).
Why Circular Linked List?¶
- The NULL assignment is not required because a node always points to another node.
- The starting point can be set to any node.
- Traversal from the first node to the last node is quick.
Circular Linked List Applications¶
- It is used in multiplayer games to give a chance to each player to play the game.
- Multiple running applications can be placed in a circular linked list on an operating system. The os keeps on iterating over these applications.
Double Linked List¶
- Btech Smart Class
- Data Structures Tutorials - Double Linked List with an example program
- Geeks for Geeks
- Doubly Linked List | Set 1 (Introduction and Insertion) - GeeksforGeeks
- Visual Algo
- Linked List (Single, Doubly), Stack, Queue, Deque - VisuAlgo
Double Linked List¶
- In this tutorial, you will learn about the doubly linke list and its implementation in Python, Java, C, and C++.
Note: Before you proceed further, make sure to learn about pointers and structs.
Double Linked List¶
- A doubly linked list is a type of linked list in which each node consists of 3 components:
*prev- address of the previous nodedata- data item*next- address of next node

Representation of Doubly Linked List¶
Let's see how we can represent a doubly linked list on an algorithm/code. Suppose we have a doubly linked list:

Representation of Doubly Linked List¶
Here, the single node is represented as
Each struct node has a data item, a pointer to the previous struct node, and a pointer to the next struct node.
Representation of Doubly Linked List¶
Now we will create a simple doubly linked list with three items to understand how this works.
/* Initialize nodes */
struct node *head;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;
/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));
Representation of Doubly Linked List¶
/* Assign data values */
one->data = 1;
two->data = 2;
three->data = 3;
/* Connect nodes */
one->next = two;
one->prev = NULL;
two->next = three;
two->prev = one;
three->next = NULL;
three->prev = two;
/* Save address of first node in head */
head = one;
Representation of Doubly Linked List¶
- In the above code,
one,two, andthreeare the nodes with data items 1, 2, and 3 respectively.- For node one:
nextstores the address oftwoandprevstoresnull(there is no node before it) - For node two:
nextstores the address ofthreeandprevstores the address ofone - For node three:
nextstoresnull(there is no node after it) andprevstores the address oftwo.
- For node one:
- Note: In the case of the head node,
prevpoints tonull, and in the case of the tail pointer,nextpoints to null. Here,oneis a head node andthreeis a tail node.
Insertion on a Doubly Linked List¶
Pushing a node to a doubly-linked list is similar to pushing a node to a linked list, but extra work is required to handle the pointer to the previous node.
We can insert elements at 3 different positions of a doubly-linked list:
Insertion on a Doubly Linked List¶
Suppose we have a double-linked list with elements 1, 2, and 3.

1. Insertion at the Beginning¶
- Let's add a node with value 6 at the beginning of the doubly linked list we made above.
-
- Create a new node
- allocate memory for
newNode - assign the data to
newNode.
-

1. Insertion at the Beginning¶
-
- Set prev and next pointers of new node
- point
nextofnewNodeto the first node of the doubly linked list - point
prevtonull

- Reorganize the pointers (changes are denoted by purple arrows)
1. Insertion at the Beginning¶
-
- Make new node as head node
- Point
prevof the first node tonewNode(now the previousheadis the second node) - Point
headtonewNode

- Reorganize the pointers
Code for Insertion at the Beginning¶
// insert node at the front
void insertFront(struct Node** head, int data) {
// allocate memory for newNode
struct Node* newNode = new Node;
// assign data to newNode
newNode->data = data;
// point next of newNode to the first node of the doubly linked list
newNode->next = (*head);
// point prev to NULL
newNode->prev = NULL;
// point previous of the first node (now first node is the second node) to newNode
if ((*head) != NULL)
(*head)->prev = newNode;
// head points to newNode
(*head) = newNode;
}
2. Insertion in between two nodes¶
- Let's add a node with value 6 after node with value 1 in the doubly linked list.
-
- Create a new node
- allocate memory for
newNode - assign the data to
newNode.

2. Insertion in between two nodes¶
-
- Set the next pointer of new node and previous node
- assign the value of
nextfrom previous node to thenextofnewNode - assign the address of
newNodeto thenextof previous node

- Reorganize the pointers
2. Insertion in between two nodes¶
-
- Set the prev pointer of new node and the next node**
- assign the value of
prevof next node to theprevofnewNode - assign the address of
newNodeto theprevof next node

- Reorganize the pointers
2. Insertion in between two nodes¶
- The final doubly linked list is after this insertion is

- Final list
Code for Insertion in between two Nodes¶
// insert a node after a specific node
void insertAfter(struct Node* prev_node, int data) {
// check if previous node is NULL
if (prev_node == NULL) {
cout << "previous node cannot be NULL";
return;
}
// allocate memory for newNode
struct Node* newNode = new Node;
// assign data to newNode
newNode->data = data;
// set next of newNode to next of prev node
newNode->next = prev_node->next;
// set next of prev node to newNode
prev_node->next = newNode;
// set prev of newNode to the previous node
newNode->prev = prev_node;
// set prev of newNode's next to newNode
if (newNode->next != NULL)
newNode->next->prev = newNode;
}
3. Insertion at the End¶
- Let's add a node with value 6 at the end of the doubly linked list.
-
- Create a new node

3. Insertion at the End¶
-
- Set prev and next pointers of new node and the previous node
- If the linked list is empty, make the
newNodeas the head node. Otherwise, traverse to the end of the doubly linked list and

- Reorganize the pointers
3. Insertion at the End¶
- The final doubly linked list looks like this.

- The final list
Code for Insertion at the End¶
// insert a newNode at the end of the list
void insertEnd(struct Node** head, int data) {
// allocate memory for node
struct Node* newNode = new Node;
// assign data to newNode
newNode->data = data;
// assign NULL to next of newNode
newNode->next = NULL;
// store the head node temporarily (for later use)
struct Node* temp = *head;
// if the linked list is empty, make the newNode as head node
if (*head == NULL) {
newNode->prev = NULL;
*head = newNode;
return;
}
// if the linked list is not empty, traverse to the end of the linked list
while (temp->next != NULL)
temp = temp->next;
// now, the last node of the linked list is temp
// point the next of the last node (temp) to newNode.
temp->next = newNode;
// assign prev of newNode to temp
newNode->prev = temp;
}
Deletion from a Doubly Linked List¶
- Similar to insertion, we can also delete a node from 3 different positions of a doubly linked list.
- Suppose we have a double-linked list with elements 1, 2, and 3.

- Original doubly linked list
Deletion from a Doubly Linked List¶
-
- Delete the First Node of Doubly Linked List
- If the node to be deleted (i.e.
del_node) is at the beginning - Reset value node after the del_node (i.e. node two)

- Reorganize the pointers
Deletion from a Doubly Linked List¶
- Finally, free the memory of
del_node. And, the linked will look like this

- Final list
Code for Deletion of the First Node¶
if (*head == del_node)
*head = del_node->next;
if (del_node->prev != NULL)
del_node->prev->next = del_node->next;
free(del);
¶
if (*head == del_node)
*head = del_node->next;
if (del_node->prev != NULL)
del_node->prev->next = del_node->next;
free(del);
2. Deletion of the Inner Node¶
- If
del_nodeis an inner node (second node), we must have to reset the value ofnextandprevof the nodes before and after thedel_node.- For the node before the del_node (i.e. first node)
- Assign the value of
nextofdel_nodeto thenextof thefirstnode.
- Assign the value of
- For the node after the del_node (i.e. third node)
- Assign the value of
prevofdel_nodeto theprevof thethirdnode.
- Assign the value of
- For the node before the del_node (i.e. first node)
2. Deletion of the Inner Node¶

- Reorganize the pointers
2. Deletion of the Inner Node¶
- Finally, we will free the memory of
del_node. And, the final doubly linked list looks like this.

- Final list
Code for Deletion of the Inner Node¶
if (del_node->next != NULL)
del_node->next->prev = del_node->prev;
if (del_node->prev != NULL)
del_node->prev->next = del_node->next;
3. Delete the Last Node of Doubly Linked List¶
- In this case, we are deleting the last node with value 3 of the doubly linked list.
- Here, we can simply delete the
del_nodeand make thenextof node beforedel_nodepoint toNULL.

- Reorganize the pointers
3. Delete the Last Node of Doubly Linked List¶
- The final doubly linked list looks like this.

- Final list
Code for Deletion of the Last Node¶
Here, del_node ->next is NULL so del_node->prev->next = NULL.
Note: We can also solve this using the first condition (for the node before del_node) of the second case (Delete the inner node).
Doubly Linked List Code in C¶
#include <stdio.h>
#include <stdlib.h>
// node creation
struct Node {
int data;
struct Node* next;
struct Node* prev;
};
...
Doubly Linked List Code in C¶
// insert node at the front
void insertFront(struct Node** head, int data) {
// allocate memory for newNode
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// assign data to newNode
newNode->data = data;
// make newNode as a head
newNode->next = (*head);
// assign null to prev
newNode->prev = NULL;
// previous of head (now head is the second node) is newNode
if ((*head) != NULL)
(*head)->prev = newNode;
// head points to newNode
(*head) = newNode;
}
...
Doubly Linked List Code in C¶
// insert a node after a specific node
void insertAfter(struct Node* prev_node, int data) {
// check if previous node is null
if (prev_node == NULL) {
printf("previous node cannot be null");
return;
}
// allocate memory for newNode
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// assign data to newNode
newNode->data = data;
// set next of newNode to next of prev node
newNode->next = prev_node->next;
// set next of prev node to newNode
prev_node->next = newNode;
// set prev of newNode to the previous node
newNode->prev = prev_node;
// set prev of newNode's next to newNode
if (newNode->next != NULL)
newNode->next->prev = newNode;
}
...
Doubly Linked List Code in C¶
// insert a newNode at the end of the list
void insertEnd(struct Node** head, int data) {
// allocate memory for node
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
// assign data to newNode
newNode->data = data;
// assign null to next of newNode
newNode->next = NULL;
// store the head node temporarily (for later use)
struct Node* temp = *head;
// if the linked list is empty, make the newNode as head node
if (*head == NULL) {
newNode->prev = NULL;
*head = newNode;
return;
}
// if the linked list is not empty, traverse to the end of the linked list
while (temp->next != NULL)
temp = temp->next;
// now, the last node of the linked list is temp
// assign next of the last node (temp) to newNode
temp->next = newNode;
// assign prev of newNode to temp
newNode->prev = temp;
}
...
Doubly Linked List Code in C¶
// delete a node from the doubly linked list
void deleteNode(struct Node** head, struct Node* del_node) {
// if head or del is null, deletion is not possible
if (*head == NULL || del_node == NULL)
return;
// if del_node is the head node, point the head pointer to the next of del_node
if (*head == del_node)
*head = del_node->next;
// if del_node is not at the last node, point the prev of node next to del_node to the previous of del_node
if (del_node->next != NULL)
del_node->next->prev = del_node->prev;
// if del_node is not the first node, point the next of the previous node to the next node of del_node
if (del_node->prev != NULL)
del_node->prev->next = del_node->next;
// free the memory of del_node
free(del_node);
}
...
Doubly Linked List Code in C¶
// print the doubly linked list
void displayList(struct Node* node) {
struct Node* last;
while (node != NULL) {
printf("%d->", node->data);
last = node;
node = node->next;
}
if (node == NULL)
printf("NULL\n");
}
...
Doubly Linked List Code in C¶
int main() {
// initialize an empty node
struct Node* head = NULL;
insertEnd(&head, 5);
insertFront(&head, 1);
insertFront(&head, 6);
insertEnd(&head, 9);
// insert 11 after head
insertAfter(head, 11);
// insert 15 after the seond node
insertAfter(head->next, 15);
displayList(head);
// delete the last node
deleteNode(&head, head->next->next->next->next->next);
displayList(head);
}
Doubly Linked List Code in C++¶
#include <iostream>
using namespace std;
// node creation
struct Node {
int data;
struct Node* next;
struct Node* prev;
};
...
Doubly Linked List Code in C++¶
// insert node at the front
void insertFront(struct Node** head, int data) {
// allocate memory for newNode
struct Node* newNode = new Node;
// assign data to newNode
newNode->data = data;
// make newNode as a head
newNode->next = (*head);
// assign null to prev
newNode->prev = NULL;
// previous of head (now head is the second node) is newNode
if ((*head) != NULL)
(*head)->prev = newNode;
// head points to newNode
(*head) = newNode;
}
...
Doubly Linked List Code in C++¶
// insert a node after a specific node
void insertAfter(struct Node* prev_node, int data) {
// check if previous node is null
if (prev_node == NULL) {
cout << "previous node cannot be null";
return;
}
// allocate memory for newNode
struct Node* newNode = new Node;
// assign data to newNode
newNode->data = data;
// set next of newNode to next of prev node
newNode->next = prev_node->next;
// set next of prev node to newNode
prev_node->next = newNode;
// set prev of newNode to the previous node
newNode->prev = prev_node;
// set prev of newNode's next to newNode
if (newNode->next != NULL)
newNode->next->prev = newNode;
}
...
Doubly Linked List Code in C++¶
// insert a newNode at the end of the list
void insertEnd(struct Node** head, int data) {
// allocate memory for node
struct Node* newNode = new Node;
// assign data to newNode
newNode->data = data;
// assign null to next of newNode
newNode->next = NULL;
// store the head node temporarily (for later use)
struct Node* temp = *head;
// if the linked list is empty, make the newNode as head node
if (*head == NULL) {
newNode->prev = NULL;
*head = newNode;
return;
}
// if the linked list is not empty, traverse to the end of the linked list
while (temp->next != NULL)
temp = temp->next;
// now, the last node of the linked list is temp
// assign next of the last node (temp) to newNode
temp->next = newNode;
// assign prev of newNode to temp
newNode->prev = temp;
}
...
Doubly Linked List Code in C++¶
// delete a node from the doubly linked list
void deleteNode(struct Node** head, struct Node* del_node) {
// if head or del is null, deletion is not possible
if (*head == NULL || del_node == NULL)
return;
// if del_node is the head node, point the head pointer to the next of del_node
if (*head == del_node)
*head = del_node->next;
// if del_node is not at the last node, point the prev of node next to del_node to the previous of del_node
if (del_node->next != NULL)
del_node->next->prev = del_node->prev;
// if del_node is not the first node, point the next of the previous node to the next node of del_node
if (del_node->prev != NULL)
del_node->prev->next = del_node->next;
// free the memory of del_node
free(del_node);
}
...
Doubly Linked List Code in C++¶
// print the doubly linked list
void displayList(struct Node* node) {
struct Node* last;
while (node != NULL) {
cout << node->data << "->";
last = node;
node = node->next;
}
if (node == NULL)
cout << "NULL\n";
}
...
Doubly Linked List Code in C++¶
int main() {
// initialize an empty node
struct Node* head = NULL;
insertEnd(&head, 5);
insertFront(&head, 1);
insertFront(&head, 6);
insertEnd(&head, 9);
// insert 11 after head
insertAfter(head, 11);
// insert 15 after the seond node
insertAfter(head->next, 15);
displayList(head);
// delete the last node
deleteNode(&head, head->next->next->next->next->next);
displayList(head);
}
Doubly Linked List Code in C++¶
public class DoublyLinkedList {
// node creation
Node head;
class Node {
int data;
Node prev;
Node next;
Node(int d) {
data = d;
}
}
...
Doubly Linked List Code in Java¶
// insert node at the front
public void insertFront(int data) {
// allocate memory for newNode and assign data to newNode
Node newNode = new Node(data);
// make newNode as a head
newNode.next = head;
// assign null to prev of newNode
newNode.prev = null;
// previous of head (now head is the second node) is newNode
if (head != null)
head.prev = newNode;
// head points to newNode
head = newNode;
}
...
Doubly Linked List Code in Java¶
// insert a node after a specific node
public void insertAfter(Node prev_node, int data) {
// check if previous node is null
if (prev_node == null) {
System.out.println("previous node cannot be null");
return;
}
// allocate memory for newNode and assign data to newNode
Node new_node = new Node(data);
// set next of newNode to next of prev node
new_node.next = prev_node.next;
// set next of prev node to newNode
prev_node.next = new_node;
// set prev of newNode to the previous node
new_node.prev = prev_node;
// set prev of newNode's next to newNode
if (new_node.next != null)
new_node.next.prev = new_node;
}
...
Doubly Linked List Code in Java¶
// insert a newNode at the end of the list
void insertEnd(int data) {
// allocate memory for newNode and assign data to newNode
Node new_node = new Node(data);
// store the head node temporarily (for later use)
Node temp = head;
// assign null to next of newNode
new_node.next = null;
// if the linked list is empty, make the newNode as head node
if (head == null) {
new_node.prev = null;
head = new_node;
return;
}
// if the linked list is not empty, traverse to the end of the linked list
while (temp.next != null)
temp = temp.next;
// assign next of the last node (temp) to newNode
temp.next = new_node;
// assign prev of newNode to temp
new_node.prev = temp;
}
...
Doubly Linked List Code in Java¶
// delete a node from the doubly linked list
void deleteNode(Node del_node) {
// if head or del is null, deletion is not possible
if (head == null || del_node == null) {
return;
}
// if del_node is the head node, point the head pointer to the next of del_node
if (head == del_node) {
head = del_node.next;
}
// if del_node is not at the last node, point the prev of node next to del_node
// to the previous of del_node
if (del_node.next != null) {
del_node.next.prev = del_node.prev;
}
// if del_node is not the first node, point the next of the previous node to the
// next node of del_node
if (del_node.prev != null) {
del_node.prev.next = del_node.next;
}
}
...
Doubly Linked List Code in Java¶
// print the doubly linked list
public void printlist(Node node) {
Node last = null;
while (node != null) {
System.out.print(node.data + "->");
last = node;
node = node.next;
}
System.out.println();
}
...
Doubly Linked List Code in Java¶
public static void main(String[] args) {
DoublyLinkedList doubly_ll = new DoublyLinkedList();
doubly_ll.insertEnd(5);
doubly_ll.insertFront(1);
doubly_ll.insertFront(6);
doubly_ll.insertEnd(9);
// insert 11 after head
doubly_ll.insertAfter(doubly_ll.head, 11);
// insert 15 after the seond node
doubly_ll.insertAfter(doubly_ll.head.next, 11);
doubly_ll.printlist(doubly_ll.head);
// delete the last node
doubly_ll.deleteNode(doubly_ll.head.next.next.next.next.next);
doubly_ll.printlist(doubly_ll.head);
}
}
Doubly Linked List Complexity¶
| Doubly Linked List Complexity | Time Complexity | Space Complexity |
|---|---|---|
| Insertion Operation | O(1) or O(n) | O(1) |
| Deletion Operation | O(1) | O(1) |
Doubly Linked List Complexity¶
-
- Complexity of Insertion Operation
- The insertion operations that do not require traversal have the time complexity of
O(1). - And, insertion that requires traversal has time complexity of
O(n). - The space complexity is
O(1).
-
- Complexity of Deletion Operation
- All deletion operations run with time complexity of
O(1). - And, the space complexity is
O(1).
Doubly Linked List Applications¶
- Redo and undo functionality in software.
- Forward and backward navigation in browsers.
- For navigation systems where forward and backward navigation is required.
Singly Linked List Vs Doubly Linked List¶
| Singly Linked List | Doubly Linked List |
|---|---|
| Each node consists of a data value and a pointer to the next node. | Each node consists of a data value, a pointer to the next node, and a pointer to the previous node. |
| Traversal can occur in one way only (forward direction). | Traversal can occur in both ways. |
| It requires less space. | It requires more space because of an extra pointer. |
| It can be implemented on the stack. | It has multiple usages. It can be implemented on the stack, heap, and binary tree. |
XOR Linked List¶
- Wikipedia
- XOR linked list - Wikipedia
- Release Dawn · ManosPapadakis95/Listes · GitHub
- Geeks for Geeks
- XOR Linked List - A Memory Efficient Doubly Linked List | Set 1 - GeeksforGeeks
- Geeks for Geeks
- XOR Linked List – A Memory Efficient Doubly Linked List | Set 2 - GeeksforGeeks
XOR Linked List¶
An ordinary doubly linked list stores addresses of the previous and next list items in each list node, requiring two address fields:
XOR Linked List¶
An XOR linked list compresses the same information into one address field by storing the bitwise XOR (here denoted by ⊕) of the address for previous and the address for next in one field:
XOR Linked List¶
More formally:
When traversing the list from left to right: supposing the cursor is at C, the previous item, B, may be XORed with the value in the link field (B⊕D). The address for D will then be obtained and list traversal may resume. The same pattern applies in the other direction.
XOR Linked List¶
so
since
since
XOR Linked List¶
The XOR operation cancels addr(B) appearing twice in the equation and all we are left with is the addr(D).
To start traversing the list in either direction from some point, the address of two consecutive items is required. If the addresses of the two consecutive items are reversed, list traversal will occur in the opposite direction.[1]
Theory of operation¶
The key is the first operation, and the properties of XOR:
Theory of operation¶
The R2 register always contains the XOR of the address of current item C with the address of the predecessor item P: C⊕P. The Link fields in the records contain the XOR of the left and right successor addresses, say L⊕R. XOR of R2 (C⊕P) with the current link field (L⊕R) yields C⊕P⊕L⊕R.
- If the predecessor was L, the P(=L) and L cancel out leaving C⊕R.
- If the predecessor had been R, the P(=R) and R cancel, leaving C⊕L.
In each case, the result is the XOR of the current address with the next address. XOR of this with the current address in R1 leaves the next address. R2 is left with the requisite XOR pair of the (now) current address and the predecessor.
XOR Linked List, C++ Doubly Linked List¶
// C++ Implementation of Memory efficient Doubly Linked List
// Importing libraries
#include <bits/stdc++.h>
#include <cinttypes>
using namespace std;
// Class 1
// Helper class(Node structure)
class Node {
public : int data;
// Xor of next node and previous node
Node* xnode;
};
XOR Linked List, C++ Doubly Linked List¶
// Method 1
// It returns Xored value of the node addresses
Node* Xor(Node* x, Node* y)
{
return reinterpret_cast<Node*>(
reinterpret_cast<uintptr_t>(x)
^ reinterpret_cast<uintptr_t>(y));
}
XOR Linked List, C++ Doubly Linked List¶
// Method 2
// Insert a node at the start of the Xored LinkedList and
// mark the newly inserted node as head
void insert(Node** head_ref, int data)
{
// Allocate memory for new node
Node* new_node = new Node();
new_node -> data = data;
// Since new node is inserted at the
// start , xnode of new node will always be
// Xor of current head and NULL
new_node -> xnode = *head_ref;
// If linkedlist is not empty, then xnode of
// present head node will be Xor of new node
// and node next to current head */
if (*head_ref != NULL) {
// *(head_ref)->xnode is Xor of (NULL and next).
// If we Xor Null with next we get next
(*head_ref)
-> xnode = Xor(new_node, (*head_ref) -> xnode);
}
// Change head
*head_ref = new_node;
}
XOR Linked List, C++ Doubly Linked List¶
// Method 3
// It simply prints contents of doubly linked
// list in forward direction
void printList(Node* head)
{
Node* curr = head;
Node* prev = NULL;
Node* next;
cout << "The nodes of Linked List are: \n";
// Till condition holds true
while (curr != NULL) {
// print current node
cout << curr -> data << " ";
// get address of next node: curr->xnode is
// next^prev, so curr->xnode^prev will be
// next^prev^prev which is next
next = Xor(prev, curr -> xnode);
// update prev and curr for next iteration
prev = curr;
curr = next;
}
}
XOR Linked List, C++ Doubly Linked List¶
// Method 4
// main driver method
int main()
{
Node* head = NULL;
insert(&head, 10);
insert(&head, 100);
insert(&head, 1000);
insert(&head, 10000);
// Printing the created list
printList(head);
return (0);
}
Skip List¶
- Wikipedia
- Skip list - Wikipedia
- Geeks for Geeks
- Skip List | Set 1 (Introduction) - GeeksforGeeks
- Skip List | Set 2 (Insertion) - GeeksforGeeks
- Skip List | Set 3 (Searching and Deletion) - GeeksforGeeks
Skip List¶
- Can we search in a sorted linked list better than O(n) time?
- The worst-case search time for a sorted linked list is O(n) as we can only linearly traverse the list and cannot skip nodes while searching.
- For a Balanced Binary Search Tree, we skip almost half of the nodes after one comparison with the root.
- For a sorted array, we have random access and we can apply Binary Search on arrays.
Skip List¶
- Can we augment sorted linked lists to search faster?
- The answer is Skip List.
- The idea is simple,
- we create multiple layers so that we can skip some nodes.
Skip List¶
- See the following example list with 16 nodes and two layers.

Skip List¶
- The upper layer works as an “express lane” that connects only the main outer stations, and the lower layer works as a “normal lane” that connects every station.
- Suppose we want to search for 50, we start from the first node of the “express lane” and keep moving on the “express lane” till we find a node whose next is greater than 50. - Once we find such a node (30 is the node in the following example) on “express lane”, we move to “normal lane” using a pointer from this node, and linearly search for 50 on “normal lane”.
- In the following example, we start from 30 on the “normal lane” and with linear search, we find 50.
What is the time complexity with two layers?¶
- worst-case case time complexity is several nodes on the “express lane” plus several nodes in a segment (A segment is several “normal lane” nodes between two “express lane” nodes) of the “normal lane”.
- So if we have \(n\) nodes on “normal lane”, \(\sqrt(n)\) (square root of \(n\)) nodes on “express lane” and we equally divide the “normal lane”,
- then there will be \(\sqrt(n)\) nodes in every segment of “normal lane”.
- √n is an optimal division with two layers.
- With this arrangement, the number of nodes traversed for a search will be
- \(O(\sqrt(n))\).
- Therefore, with \(O(\sqrt(n))\) extra space, we can reduce the time complexity to
- \(O(\sqrt(n))\).
Advantages of Skip List¶
- The skip list is solid and trustworthy.
- To add a new node to it, it will be inserted extremely quickly.
- Easy to implement compared to the hash table and binary search tree
- The number of nodes in the skip list increases, and the possibility of the worst-case decreases
- Requires only \(\theta(logn)\) time in the average case for all operations.
- Finding a node in the list is relatively straightforward.
Disadvantages of Skip List¶
- It needs a greater amount of memory than the balanced tree.
- Reverse search is not permitted.
- Searching is slower than a linked list
- Skip lists are not cache-friendly because they don’t optimize the locality of reference
Deciding nodes level¶
Each element in the list is represented by a node, the level of the node is chosen randomly while insertion in the list. **Level does not depend on the number of elements in the node.
The level for node is decided by the following algorithm¶
randomLevel()
lvl := 1
//random() that returns a random value in [0...1)
while random() < p and lvl < MaxLevel do
lvl := lvl + 1
return lvl
MaxLevel is the upper bound on number of levels in the skip list.¶
- It can be determined as – \(L(N) = log_{p/2}{N}\).
- Above algorithm assure that random level will never be greater than MaxLevel.
- Here \(p\) is the fraction of the nodes with level \(i\) pointers
- Also having level \(i+1\) pointers and \(N\) is the number of nodes in the list.
Node Structure¶
- Each node carries a key and a forward array carrying pointers to nodes of a different level. A level \(i\) node carries \(i\) forward pointers indexed through \(0\) to \(i\).

Insertion in Skip List¶
- We will start from the highest level in the list and compare the key of the next node of the current node with the key to be inserted. The basic idea is If
-
- Key of next node is less than key to be inserted then we keep on moving forward on the same level
-
- Key of next node is greater than the key to be inserted then we store the pointer to current node i at update[i] and move one level down and continue our search.
-
- At the level 0, we will definitely find a position to insert the given key.
Insertion in Skip List Algorithm¶
Following is the pseudo-code for the insertion algorithm
**Insert(list, searchKey)**
local update[0...MaxLevel+1]
x := list -> header
for i := list -> level downto 0 do
while x -> forward[i] -> key forward[i]
update[i] := x
x := x -> forward[0]
lvl := randomLevel()
if lvl > list -> level then
for i := list -> level + 1 to lvl do
update[i] := list -> header
list -> level := lvl
x := makeNode(lvl, searchKey, value)
for i := 0 to level do
x -> forward[i] := update[i] -> forward[i]
update[i] -> forward[i] := x
Insertion in Skip List Algorithm¶
- Here \(update[i]\) holds the pointer to node at level \(i\) from which we moved down to level \(i-1\) and pointer of node left to insertion position at level \(0\).
- Consider this example where we want to insert key \(17\)
Insertion in Skip List Algorithm¶

Insertion in Skip List in C++¶
- Following is the code for insertion of key in Skip list
// C++ code for inserting element in skip list
#include <bits/stdc++.h>
using namespace std;
// Class to implement node
class Node
{
public:
int key;
// Array to hold pointers to node of different level
Node **forward;
Node(int, int);
};
...
Insertion in Skip List in C++¶
Node::Node(int key, int level)
{
this->key = key;
// Allocate memory to forward
forward = new Node*[level+1];
// Fill forward array with 0(NULL)
memset(forward, 0, sizeof(Node*)*(level+1));
};
...
Insertion in Skip List in C++¶
// Class for Skip list
class SkipList
{
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node *header;
public:
SkipList(int, float);
int randomLevel();
Node* createNode(int, int);
void insertElement(int);
void displayList();
};
...
Insertion in Skip List in C++¶
SkipList::SkipList(int MAXLVL, float P)
{
this->MAXLVL = MAXLVL;
this->P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
};
...
Insertion in Skip List in C++¶
// create random level for node
int SkipList::randomLevel()
{
float r = (float)rand()/RAND_MAX;
int lvl = 0;
while (r < P && lvl < MAXLVL)
{
lvl++;
r = (float)rand()/RAND_MAX;
}
return lvl;
};
...
Insertion in Skip List in C++¶
// create new node
Node* SkipList::createNode(int key, int level)
{
Node *n = new Node(key, level);
return n;
};
...
Insertion in Skip List in C++¶
// Insert given key in skip list
void SkipList::insertElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for (int i = level; i >= 0; i--)
{
while (current->forward[i] != NULL &&
current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
/* reached level 0 and forward pointer to
right, which is desired position to
insert key.
*/
current = current->forward[0];
...
Insertion in Skip List in C++¶
...
/* if current is NULL that means we have reached
to end of the level or current's key is not equal
to key to insert that means we have to insert
node between update[0] and current node */
if (current == NULL || current->key != key)
{
// Generate a random level for node
int rlevel = randomLevel();
// If random level is greater than list's current
// level (node with highest level inserted in
// list so far), initialize update value with pointer
// to header for further use
if (rlevel > level)
{
for (int i=level+1;i<rlevel+1;i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level generated
Node* n = createNode(key, rlevel);
// insert node by rearranging pointers
for (int i=0;i<=rlevel;i++)
{
n->forward[i] = update[i]->forward[i];
update[i]->forward[i] = n;
}
cout << "Successfully Inserted key " << key << "\n";
}
};
...
Insertion in Skip List in C++¶
// Display skip list level wise
void SkipList::displayList()
{
cout<<"\n*****Skip List*****"<<"\n";
for (int i=0;i<=level;i++)
{
Node *node = header->forward[i];
cout << "Level " << i << ": ";
while (node != NULL)
{
cout << node->key<<" ";
node = node->forward[i];
}
cout << "\n";
}
};
...
Insertion in Skip List in C++¶
// Driver to test above code
int main()
{
// Seed random number generator
srand((unsigned)time(0));
// create SkipList object with MAXLVL and P
SkipList lst(3, 0.5);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
}
Insertion in Skip List in Java¶
// Java code for inserting element in skip list
class GFG {
// Class to implement node
static class Node {
int key;
// Array to hold pointers to node of different level
Node forward[];
Node(int key, int level)
{
this.key = key;
// Allocate memory to forward
forward = new Node[level + 1];
}
};
...
Insertion in Skip List in Java¶
// Class for Skip list
static class SkipList {
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node header;
...
Insertion in Skip List in Java¶
SkipList(int MAXLVL, float P)
{
this.MAXLVL = MAXLVL;
this.P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
}
...
Insertion in Skip List in Java¶
int randomLevel()
{
float r = (float)Math.random();
int lvl = 0;
while (r < P && lvl < MAXLVL) {
lvl++;
r = (float)Math.random();
}
return lvl;
}
...
Insertion in Skip List in Java¶
Insertion in Skip List in Java¶
// Insert given key in skip list
void insertElement(int key)
{
Node current = header;
// create update array and initialize it
Node update[] = new Node[MAXLVL + 1];
/* start from highest level of skip list
move the current pointer forward while
key is greater than key of node next to
current Otherwise inserted current in update
and move one level down and continue search
*/
for (int i = level; i >= 0; i--) {
while (current.forward[i] != null
&& current.forward[i].key < key)
current = current.forward[i];
update[i] = current;
}
/* reached level 0 and forward pointer to
right, which is desired position to
insert key.
*/
current = current.forward[0];
...
Insertion in Skip List in Java¶
...
/* if current is NULL that means we have reached
to end of the level or current's key is not
equal to key to insert that means we have to
insert node between update[0] and current node
*/
if (current == null || current.key != key) {
// Generate a random level for node
int rlevel = randomLevel();
// If random level is greater than list's
// current level (node with highest level
// inserted in list so far), initialize
// update value with pointer to header for
// further use
if (rlevel > level) {
for (int i = level + 1; i < rlevel + 1;
i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level
// generated
Node n = createNode(key, rlevel);
// insert node by rearranging pointers
for (int i = 0; i <= rlevel; i++) {
n.forward[i] = update[i].forward[i];
update[i].forward[i] = n;
}
System.out.println(
"Successfully Inserted key " + key);
}
}
...
Insertion in Skip List in Java¶
// Display skip list level wise
void displayList()
{
System.out.println("\n*****Skip List*****");
for (int i = 0; i <= level; i++) {
Node node = header.forward[i];
System.out.print("Level " + i + ": ");
while (node != null) {
System.out.print(node.key + " ");
node = node.forward[i];
}
System.out.println();
}
}
}
...
Insertion in Skip List in Java¶
// Driver to test above code
public static void main(String[] args)
{
// create SkipList object with MAXLVL and P
SkipList lst = new SkipList(3, 0.5f);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
}
}
// This code is contributed by Lovely Jain
Output
Successfully Inserted key 3
Successfully Inserted key 6
Successfully Inserted key 7
Successfully Inserted key 9
Successfully Inserted key 12
Successfully Inserted key 19
Successfully Inserted key 17
Successfully Inserted key 26
Successfully Inserted key 21
Successfully Inserted key 25
*****Skip List*****
Level 0: 3 6 7 9 12 17 19 21 25 26
Level 1: 3 6 12 17 25 26
Level 2: 3 6 12 25
Level 3: 3 25
Note: The level of nodes is decided randomly, so output may differ.
Time complexity¶
- Average: \(O(log n)\)
- Worst: \(O(n)\)
Skip List - Searching and Deletion¶
Searching an element in Skip list¶
- Searching an element is very similar to approach for searching a spot for inserting an element in Skip list. The basic idea is if
-
- Key of next node is less than search key then we keep on moving forward on the same level.
-
- Key of next node is greater than the key to be inserted then we store the pointer to current node i at update[i] and move one level down and continue our search.
-
- At the lowest level(0), if the element next to the rightmost element (update[0]) has key equal to the search key, then we have found key otherwise failure. Following is the pseudo code for searching element –
Skip List - Searching Algorithm¶
**Search(list, searchKey)**
x := list -> header
-- loop invariant: x -> key level downto 0 do
while x -> forward[i] -> key forward[i]
x := x -> forward[0]
if x -> key = searchKey then return x -> value
else return failure
Skip List - Searching Example¶
- Consider this example where we want to search for key 17-

Deleting an element from the Skip list¶
- Deletion of an element k is preceded by locating element in the Skip list using above mentioned search algorithm.
- Once the element is located, rearrangement of pointers is done to remove element form list just like we do in singly linked list.
- We start from lowest level and do rearrangement until element next to update[i] is not k. - After deletion of element there could be levels with no elements,
- so we will remove these levels as well by decrementing the level of Skip list.
Skip List - Deletion Algorithm¶
**Delete(list, searchKey)**
local update[0..MaxLevel+1]
x := list -> header
for i := list -> level downto 0 do
while x -> forward[i] -> key forward[i]
update[i] := x
x := x -> forward[0]
if x -> key = searchKey then
for i := 0 to list -> level do
if update[i] -> forward[i] ≠ x then break
update[i] -> forward[i] := x -> forward[i]
free(x)
while list -> level > 0 and list -> header -> forward[list -> level] = NIL do
list -> level := list -> level – 1
Skip List - Deletion Example¶
- Consider this example where we want to delete element 6

- Here at level 3, there is no element (arrow in red) after deleting element 6.
- So we will decrement level of skip list by 1.
Skip List - Deletion in C++¶
// C++ code for searching and deleting element in skip list
#include <bits/stdc++.h>
using namespace std;
// Class to implement node
class Node
{
public:
int key;
// Array to hold pointers to node of different level
Node **forward;
Node(int, int);
};
...
Skip List - Deletion in C++¶
Node::Node(int key, int level)
{
this->key = key;
// Allocate memory to forward
forward = new Node*[level+1];
// Fill forward array with 0(NULL)
memset(forward, 0, sizeof(Node*)*(level+1));
};
...
Skip List - Deletion in C++¶
// Class for Skip list
class SkipList
{
// Maximum level for this skip list
int MAXLVL;
// P is the fraction of the nodes with level
// i pointers also having level i+1 pointers
float P;
// current level of skip list
int level;
// pointer to header node
Node *header;
...
Skip List - Deletion in C++¶
...
public:
SkipList(int, float);
int randomLevel();
Node* createNode(int, int);
void insertElement(int);
void deleteElement(int);
void searchElement(int);
void displayList();
};
...
Skip List - Deletion in C++¶
SkipList::SkipList(int MAXLVL, float P)
{
this->MAXLVL = MAXLVL;
this->P = P;
level = 0;
// create header node and initialize key to -1
header = new Node(-1, MAXLVL);
};
...
Skip List - Deletion in C++¶
// create random level for node
int SkipList::randomLevel()
{
float r = (float)rand()/RAND_MAX;
int lvl = 0;
while(r < P && lvl < MAXLVL)
{
lvl++;
r = (float)rand()/RAND_MAX;
}
return lvl;
};
...
Skip List - Deletion in C++¶
// create new node
Node* SkipList::createNode(int key, int level)
{
Node *n = new Node(key, level);
return n;
};
...
Skip List - Deletion in C++¶
// Insert given key in skip list
void SkipList::insertElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for(int i = level; i >= 0; i--)
{
while(current->forward[i] != NULL &&
current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
...
Skip List - Deletion in C++¶
...
/* reached level 0 and forward pointer to
right, which is desired position to
insert key.
*/
current = current->forward[0];
/* if current is NULL that means we have reached
to end of the level or current's key is not equal
to key to insert that means we have to insert
node between update[0] and current node */
if (current == NULL || current->key != key)
{
// Generate a random level for node
int rlevel = randomLevel();
/* If random level is greater than list's current
level (node with highest level inserted in
list so far), initialize update value with pointer
to header for further use */
if(rlevel > level)
{
for(int i=level+1;i<rlevel+1;i++)
update[i] = header;
// Update the list current level
level = rlevel;
}
// create new node with random level generated
Node* n = createNode(key, rlevel);
// insert node by rearranging pointers
for(int i=0;i<=rlevel;i++)
{
n->forward[i] = update[i]->forward[i];
update[i]->forward[i] = n;
}
cout<<"Successfully Inserted key "<<key<<"\n";
}
};
...
Skip List - Deletion in C++¶
// Delete element from skip list
void SkipList::deleteElement(int key)
{
Node *current = header;
// create update array and initialize it
Node *update[MAXLVL+1];
memset(update, 0, sizeof(Node*)*(MAXLVL+1));
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for(int i = level; i >= 0; i--)
{
while(current->forward[i] != NULL &&
current->forward[i]->key < key)
current = current->forward[i];
update[i] = current;
}
...
Skip List - Deletion in C++¶
...
/* reached level 0 and forward pointer to
right, which is possibly our desired node.*/
current = current->forward[0];
// If current node is target node
if(current != NULL and current->key == key)
{
/* start from lowest level and rearrange
pointers just like we do in singly linked list
to remove target node */
for(int i=0;i<=level;i++)
{
/* If at level i, next node is not target
node, break the loop, no need to move
further level */
if(update[i]->forward[i] != current)
break;
update[i]->forward[i] = current->forward[i];
}
// Remove levels having no elements
while(level>0 &&
header->forward[level] == 0)
level--;
cout<<"Successfully deleted key "<<key<<"\n";
}
};
...
Skip List - Deletion in C++¶
// Search for element in skip list
void SkipList::searchElement(int key)
{
Node *current = header;
/* start from highest level of skip list
move the current pointer forward while key
is greater than key of node next to current
Otherwise inserted current in update and
move one level down and continue search
*/
for(int i = level; i >= 0; i--)
{
while(current->forward[i] &&
current->forward[i]->key < key)
current = current->forward[i];
}
/* reached level 0 and advance pointer to
right, which is possibly our desired node*/
current = current->forward[0];
// If current node have key equal to
// search key, we have found our target node
if(current and current->key == key)
cout<<"Found key: "<<key<<"\n";
};
...
Skip List - Deletion in C++¶
// Display skip list level wise
void SkipList::displayList()
{
cout<<"\n*****Skip List*****"<<"\n";
for(int i=0;i<=level;i++)
{
Node *node = header->forward[i];
cout<<"Level "<<i<<": ";
while(node != NULL)
{
cout<<node->key<<" ";
node = node->forward[i];
}
cout<<"\n";
}
};
...
Skip List - Deletion in C++¶
// Driver to test above code
int main()
{
// Seed random number generator
srand((unsigned)time(0));
// create SkipList object with MAXLVL and P
SkipList lst(3, 0.5);
lst.insertElement(3);
lst.insertElement(6);
lst.insertElement(7);
lst.insertElement(9);
lst.insertElement(12);
lst.insertElement(19);
lst.insertElement(17);
lst.insertElement(26);
lst.insertElement(21);
lst.insertElement(25);
lst.displayList();
//Search for node 19
lst.searchElement(19);
//Delete node 19
lst.deleteElement(19);
lst.displayList();
}
Output¶
Successfully Inserted key 3
Successfully Inserted key 6
Successfully Inserted key 7
Successfully Inserted key 9
Successfully Inserted key 12
Successfully Inserted key 19
Successfully Inserted key 17
Successfully Inserted key 26
Successfully Inserted key 21
Successfully Inserted key 25
*****Skip List*****
Level 0: 3 6 7 9 12 17 19 21 25 26
Level 1: 6 9 19 26
Level 2: 19
Found key: 19
Successfully deleted key 19
*****Skip List*****
Level 0: 3 6 7 9 12 17 21 25 26
Level 1: 6 9 26
Time complexity of both searching and deletion (same)¶
- Time complexity Worst case
- Access – \(O(n)\)
- Search – \(O(n)\)
- Insert – \(O(n)\)
- Space – \(O(nlogn)\)
- Delete – \(O(n)\)
Strand Sort¶
- Geeks for Geeks
- Strand Sort - GeeksforGeeks
Strand Sort¶
- Strand sort is a recursive sorting algorithm that sorts items of a list into increasing order.
- It has \(O(n^2)\) worst time complexity
- which occurs when the input list is reverse sorted.
- It has a best case time complexity of \(O(n)\)
- which occurs when the input is a list that is already sorted.
Strand Sort Example¶
- Given a list of items, sort them in increasing order.
- Input:
- Output
Strand Sort Example¶
- Given a list of items, sort them in increasing order.
- Input:
- Output
Strand Sort Example¶
-
Let,
input[] = {10, 5, 30, 40, 2, 4, 9} -
Initialize:
output[] = {}, sublist[] = {}
Strand Sort Example¶
- Move first item of input to sublist.
sublist[] = {10} - Traverse remaining items of input and if current element is greater than last item of sublist, move this item from input to sublist.
- Now,
sublist[] = {10, 30, 40}, input[] = {5, 2, 4, 9} - Merge sublist into output.
op = {10, 30, 40}
Strand Sort Example¶
- Next recursive call
- Move first item of input to sublist.
sublist[] = {5}
- Move first item of input to sublist.
- Traverse remaining items of input and move elements greater than last inserted.
input[] = {2, 4}
sublist[] = {5, 9} - Merge sublist into op.
output = {5, 9, 10, 30, 40} - Last Recursive Call
{2, 4}are first moved to sublist and then merged into output.
output = {2, 4, 5, 9, 10, 30, 40}
Steps used in the Strand Sort Algorithm¶
- Let
ip[]be input list andop[]be output list. - Create an empty sublist and move first item of
ip[]to it. - Traverse remaining items of ip. For every item
x, check ifxis greater than last inserted item to sublist. If yes, removexfromip[]and add at the end of sublist. If no, ignorex(Keep it, it inip[]) - Merge sublist into
op[](output list) - Recur for remaining items in
ip[]and current items inop[].
Strand Sort in C++¶
// CPP program to implement Strand Sort
#include <bits/stdc++.h>
using namespace std;
// A recursive function to implement Strand
// sort.
// ip is input list of items (unsorted).
// op is output list of items (sorted)
void strandSort(list<int> &ip, list<int> &op)
{
// Base case : input is empty
if (ip.empty())
return;
// Create a sorted sublist with
// first item of input list as
// first item of the sublist
list<int> sublist;
sublist.push_back(ip.front());
ip.pop_front();
...
Strand Sort in C++¶
...
// Traverse remaining items of ip list
for (auto it = ip.begin(); it != ip.end(); ) {
// If current item of input list
// is greater than last added item
// to sublist, move current item
// to sublist as sorted order is
// maintained.
if (*it > sublist.back()) {
sublist.push_back(*it);
// erase() on list removes an
// item and returns iterator to
// next of removed item.
it = ip.erase(it);
}
// Otherwise ignore current element
else
it++;
}
...
Strand Sort in C++¶
Strand Sort in C++¶
// Recur for remaining items in
// input and current items in op.
strandSort(ip, op);
} //end of function...
Strand Sort in C++¶
// Driver code
int main(void)
{
list<int> ip{10, 5, 30, 40, 2, 4, 9};
// To store sorted output list
list<int> op;
// Sorting the list
strandSort(ip, op);
// Printing the sorted list
for (auto x : op)
cout << x << " ";
return 0;
}
Strand Sort in C¶
Sorting algorithms/Strand sort - Rosetta Code
#include <stdio.h>
typedef struct node_t *node, node_t;
struct node_t { int v; node next; };
typedef struct { node head, tail; } slist;
...
Strand Sort in C¶
void push(slist *l, node e) {
if (!l->head) l->head = e;
if (l->tail) l->tail->next = e;
l->tail = e;
}
...
Strand Sort in C¶
node removehead(slist *l) {
node e = l->head;
if (e) {
l->head = e->next;
e->next = 0;
}
return e;
}
...
Strand Sort in C¶
Strand Sort in C¶
void merge(slist *a, slist *b) {
slist r = {0};
while (a->head && b->head)
push(&r, removehead(a->head->v <= b->head->v ? a : b));
join(&r, a->head ? a : b);
*a = r;
b->head = b->tail = 0;
}
...
Strand Sort in C¶
void sort(int *ar, int len)
{
node_t all[len];
// array to list
for (int i = 0; i < len; i++)
all[i].v = ar[i], all[i].next = i < len - 1 ? all + i + 1 : 0;
slist list = {all, all + len - 1}, rem, strand = {0}, res = {0};
for (node e = 0; list.head; list = rem) {
rem.head = rem.tail = 0;
while ((e = removehead(&list)))
push((!strand.head || e->v >= strand.tail->v) ? &strand : &rem, e);
merge(&res, &strand);
}
// list to array
for (int i = 0; res.head; i++, res.head = res.head->next)
ar[i] = res.head->v;
}
...
Strand Sort in C¶
void show(const char *title, int *x, int len)
{
printf("%s ", title);
for (int i = 0; i < len; i++)
printf("%3d ", x[i]);
putchar('\n');
}
...
Strand Sort in C¶
# define SIZE sizeof(x)/sizeof(int)
int main(void)
{
int x[] = {-2,0,-2,5,5,3,-1,-3,5,5,0,2,-4,4,2};
show("before sort:", x, SIZE);
sort(x, sizeof(x)/sizeof(int));
show("after sort: ", x, SIZE);
return 0;
}
Arrays¶
- Geeks for Geeks
- Array Data Structure - GeeksforGeeks
- Data structures Tutorials - Arrays
- Circular array - GeeksforGeeks
What is an Array?¶
- Whenever we want to work with large number of data values,
- we need to use that much number of different variables.
- As the number of variables are increasing,
- complexity of the program also increases and programmers get confused with the variable names.
- There may be situations in which we need to work with large number of similar data values. - To make this work more easy, C programming language provides a concept called "Array".
What is an Array?¶
An array is a variable which can store multiple values of same data type at a time.
An array can also be defined as follows...
"Collection of similar data items stored in continuous memory locations with single name".
To understand the concept of arrays, consider the following example declaration.
What is an Array?¶
int a, b, c
- Here, the compiler allocates 2 bytes of memory with name 'a', another 2 bytes of memory with name 'b' and more 2 bytes with name 'c'.
- These three memory locations are may be in sequence or may not be in sequence. Here these individual variables store only one value at a time.

- Now consider the following declaration...
What is an Array?¶
int a[3];
- Here, the compiler allocates total 6 bytes of continuous memory locations with single name 'a'. But allows to store three different integer values (each in 2 bytes of memory) at a time.
What is an Array?¶
- And memory is organized as follows

What is an Array?¶
- That means all these three memory locations are named as 'a'.
- But "how can we refer individual elements?" is the big question.
- Answer for this question is, compiler not only allocates memory,
- but also assigns a numerical value to each individual element of an array.
- This numerical value is called as "
Index".
What is an Array?¶
Indexvalues for the above example are as follows...

What is an Array?¶
- The individual elements of an array are identified using the combination of
nameandindexas follows...arrayName[indexValue]
- For the above example, the individual elements can be referred as follows...

What is an Array?¶
If I want to assign a value to any of these memory locations (array elements), we can assign as follows... - a[1] = 100;
The result will be as follows...

Types of Arrays in C¶
- In c programming language, arrays are classified into two types. They are as follows...
-
- Single Dimensional Array / One Dimensional Array
-
- Multi Dimensional Array
-
Single Dimensional Array¶
- In c programming language,
- single dimensional arrays are used to store list of values of same datatype.
- In other words, single dimensional arrays are used to store a row of values.
- In single dimensional array, data is stored in linear form.
- Single dimensional arrays are also called as
- one-dimensional arrays,
- Linear Arrays or simply
- 1-D Arrays.
Declaration of Single Dimensional Array¶
- We use the following general syntax for declaring a single dimensional array...
The above declaration of single dimensional array reserves 60 continuous memory locations of 2 bytes each with the name rollNumbers and tells the compiler to allow only integer values into those memory locations.
Initialization of Single Dimensional Array¶
- We use the following general syntax for declaring and initializing a single dimensional array with size and initial values.
- The above declaration of single dimensional array reserves 6 contiguous memory locations of 2 bytes each with the name marks and initializes with value
89in first memory location,90in second memory location,76in third memory location,78in fourth memory location,98in fifth memory location and86in sixth memory location.
Initialization of Single Dimensional Array¶
- We can also use the following general syntax to intialize a single dimensional array without specifying size and with initial values.
The array must be initialized if it is created without specifying any size. In this case, the size of the array is decided based on the number of values initialized
Initialization of Single Dimensional Array¶
- In the above example declaration, size of the array
marksis6and the size of the arraystudentNameis16. - This is because in case of character array, compiler stores one exttra character called
\0(NULL)at the end.
Accessing Elements of Single Dimensional Array¶
- In c programming language, to access the elements of single dimensional array we use array name followed by index value of the element that to be accessed.
- Here the index value must be enclosed in square braces.
Indexvalue of an element in an array is the reference number given to each element at the time of memory allocation.- The index value of single dimensional array starts with zero (0) for first element and incremented by one for each element.
- The index value in an array is also called as
subscriptorindices.
Accessing Elements of Single Dimensional Array¶
- We use the following general syntax to access individual elements of single dimensional array...
- In the above statement, the third element of 'marks' array is assinged with value '99'.
Multi Dimensional Array¶
- An array of arrays is called as multi dimensional array.
- In simple words, an array created with more than one dimension (size) is called as multi dimensional array.
- Multi dimensional array can be of two dimensional array or three dimensional array or four dimensional array or more
- Most popular and commonly used multi dimensional array is two dimensional array. The 2-D arrays are used to store data in the form of table.
- We also use 2-D arrays to create mathematical matrices.
Declaration of Two Dimensional Array¶
- We use the following general syntax for declaring a two dimensional array
- The above declaration of two dimensional array reserves 6 continuous memory locations of 2 bytes each in the form of 2 rows and 3 columns.
Initialization of Two Dimensional Array¶
- We use the following general syntax for declaring and initializing a two dimensional array with specific number of rows and coloumns with initial values
- The above declaration of two-dimensional array reserves 6 contiguous memory locations of 2 bytes each in the form of 2 rows and 3 columns.
- And the first row is initialized with values 1, 2 & 3 and second row is initialized with values 4, 5 & 6.
Initialization of Two Dimensional Array¶
We can also initialize as follows...
Accessing Individual Elements of Two Dimensional Array¶
- In a c programming language, to access elements of a two-dimensional array we use array name followed by row index value and column index value of the element that to be accessed.
- Here the row and column index values must be enclosed in separate square braces.
- In case of the two-dimensional array the compiler assigns separate index values for rows and columns.
- We use the following general syntax to access the individual elements of a two-dimensional array...
- In the above statement, the element with row index 0 and column index 1 of matrix_A array is assinged with value 10.
Circular Array¶
- An array is called circular if we consider the first element as next of the last element.
- Circular arrays are used to implement queue (Refer to this and this).
Circular Array¶
An example problem :
Suppose n people are sitting at a circular table with names A, B, C, D, ... Given a name, we need to print all n people (in order) starting from the given name.
Circular Array¶
- For example, consider \(6\) people \(A \ B \ C \ D \ E \ F\) and given name as \(D\). People sitting in a circular manner starting from \(D\) are \(D \ E \ F \ A \ B \ C\).
- A simple solution is to create an auxiliary array of size \(2 \times n\) and store it in another array. For example for \(6\) people, we create below the auxiliary array.
- \(A \ B \ C \ D \ E \ F \ A \ B \ C \ D \ E \ F\)
-
Now for any given index, we simply print n elements starting from it. For example, we print the following \(6\).
-
A B C D E F A B C D E F
-
Below is the implementation of the above approach.
Circular Array in C++¶
// CPP program to demonstrate use of circular
// array using extra memory space
#include <bits/stdc++.h>
using namespace std;
void print(char a[], int n, int ind)
{
// Create an auxiliary array of twice size.
char b[(2 * n)];
// Copy a[] to b[] two times
for (int i = 0; i < n; i++)
b[i] = b[n + i] = a[i];
// print from ind-th index to (n+i)th index.
for (int i = ind; i < n + ind; i++)
cout << b[i] << " ";
}
Circular Array in C++¶
// Driver code
int main()
{
char a[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
int n = sizeof(a) / sizeof(a[0]);
print(a, n, 3);
return 0;
}
Circular Array in Java¶
// Java program to demonstrate use of circular
// array using extra memory space
import java.util.*;
import java.lang.*;
public class GfG{
public static void print(char a[], int n,
int ind){
// Create an auxiliary array
// of twice size.
char[] b = new char[(2 * n)];
// Copy a[] to b[] two times
for (int i = 0; i < n; i++)
b[i] = b[n + i] = a[i];
// print from ind-th index to
// (n+i)th index.
for (int i = ind; i < n + ind; i++)
System.out.print(b[i]+" ");
}
...
Circular Array in Java¶
...
// Driver code
public static void main(String argc[]){
char[] a = new char[]{ 'A', 'B', 'C',
'D', 'E', 'F' };
int n = 6;
print(a, n, 3);
}
}
/* This code is contributed by Sagar Shukla */
Circular Array in C¶
// C# program to demonstrate use of circular
// array using extra memory space
using System;
public class GfG {
public static void print(char[] a, int n,
int ind)
{
// Create an auxiliary array
// of twice size.
char[] b = new char[(2 * n)];
// Copy a[] to b[] two times
for (int i = 0; i < n; i++)
b[i] = b[n + i] = a[i];
// print from ind-th index to
// (n+i)th index.
for (int i = ind; i < n + ind; i++)
Console.Write(b[i] + " ");
}
Circular Array in C¶
...
// Driver code
public static void Main()
{
char[] a = new char[] { 'A', 'B', 'C',
'D', 'E', 'F' };
int n = 6;
print(a, n, 3);
}
}
/* This code is contributed by vt_m*/
Array Rotations¶
- Geeks for Geeks
- Program for array rotation - GeeksforGeeks
Array Rotations¶
- Given an array of integers
arr[]of sizeNand an integer, the task is to rotate the array elements to theleftbydpositions.
Array Rotations - Example¶
Input arr[] = {1, 2, 3, 4, 5, 6, 7},d = 2
Output 3 4 5 6 7 1 2
Array Rotations - Example¶
Input: arr[] = {3, 4, 5, 6, 7, 1, 2}, d=2
Output: 5 6 7 1 2 3 4
Array Rotations¶
Approach 1 (Using temp array) - This problem can be solved using the below idea: - After rotating d positions to the left, - the first d elements become the last d elements of the array - First store the elements from index d to N-1 into the temp array. - Then store the first d elements of the original array into the temp array. - Copy back the elements of the temp array into the original array
Array Rotations¶
- Suppose the give array is arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2.
- First Step:
- => Store the elements from 2nd index to the last.
- => temp[] = [3, 4, 5, 6, 7]
- Second Step:
- => Now store the first 2 elements into the temp[] array.
- => temp[] = [3, 4, 5, 6, 7, 1, 2]
- Third Steps:
- => Copy the elements of the temp[] array into the original array.
- => arr[] = temp[] So arr[] = [3, 4, 5, 6, 7, 1, 2]
Follow the steps below to solve the given problem.
Array Rotations¶
- Initialize a temporary array(temp[n]) of length same as the original array
- Initialize an integer(k) to keep a track of the current index
- Store the elements from the position d to n-1 in the temporary array
- Now, store 0 to d-1 elements of the original array in the temporary array
- Lastly, copy back the temporary array to the original array
Array Rotations in C++¶
#include <bits/stdc++.h>
using namespace std;
// Fuction to rotate array
void Rotate(int arr[], int d, int n)
{
// Storing rotated version of array
int temp[n];
// Keepig track of the current index
// of temp[]
int k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++) {
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++) {
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
...
¶
#include <bits/stdc++.h>
using namespace std;
// Fuction to rotate array
void Rotate(int arr[], int d, int n)
{
// Storing rotated version of array
int temp[n];
// Keepig track of the current index
// of temp[]
int k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++) {
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++) {
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
...
Array Rotations in C++¶
// Function to print elements of array
void PrintTheArray(int arr[], int n)
{
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
}
...
¶
// Function to print elements of array
void PrintTheArray(int arr[], int n)
{
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
}
...
Array Rotations in C++¶
// Driver code
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int N = sizeof(arr) / sizeof(arr[0]);
int d = 2;
// Function calling
Rotate(arr, d, N);
PrintTheArray(arr, N);
return 0;
}
Array Rotations in Java¶
/*package whatever //do not write package name here */
import java.io.*;
class GFG {
// Fuction to rotate array
static void Rotate(int arr[], int d, int n)
{
// Storing rotated version of array
int temp[] = new int[n];
// Keepig track of the current index
// of temp[]
int k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++) {
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++) {
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++) {
arr[i] = temp[i];
}
}
...
Array Rotations in Java¶
// Function to print elements of array
static void PrintTheArray(int arr[], int n)
{
for (int i = 0; i < n; i++) {
System.out.print(arr[i]+" ");
}
}
public static void main (String[] args) {
int arr[] = { 1, 2, 3, 4, 5, 6, 7 };
int N = arr.length;
int d = 2;
// Function calling
Rotate(arr, d, N);
PrintTheArray(arr, N);
}
}
Array Rotations in C¶
// Include namespace system
using System;
public class GFG
{
// Fuction to rotate array
public static void Rotate(int[] arr, int d, int n)
{
// Storing rotated version of array
int[] temp = new int[n];
// Keepig track of the current index
// of temp[]
var k = 0;
// Storing the n - d elements of
// array arr[] to the front of temp[]
for (int i = d; i < n; i++)
{
temp[k] = arr[i];
k++;
}
// Storing the first d elements of array arr[]
// into temp
for (int i = 0; i < d; i++)
{
temp[k] = arr[i];
k++;
}
// Copying the elements of temp[] in arr[]
// to get the final rotated array
for (int i = 0; i < n; i++)
{
arr[i] = temp[i];
}
}
...
Array Rotations in C¶
// Function to print elements of array
public static void PrintTheArray(int[] arr, int n)
{
for (int i = 0; i < n; i++)
{
Console.Write(arr[i].ToString() + " ");
}
}
...
Array Rotations in C¶
public static void Main(String[] args)
{
int[] arr = {1, 2, 3, 4, 5, 6, 7};
var N = arr.Length;
var d = 2;
// Function calling
GFG.Rotate(arr, d, N);
GFG.PrintTheArray(arr, N);
}
}
Arrangement Rearrangement¶
- Geeks for Geeks
- Array Rearrangement - GeeksforGeeks
Arrangement Rearrangement¶
- Rearrange an array such that
arr[i] = i - Given an array of elements of length
N, ranging from0toN – 1. - All elements may not be present in the array.
- If the element is not present then there will be
-1present in the array. - Rearrange the array such that
A[i] = iand ifiis not present,- display
-1at that place.
- display
Arrangement Rearrangement - Example¶
- Input :
arr = {-1, -1, 6, 1, 9, 3, 2, -1, 4, -1} - Output :
[-1, 1, 2, 3, 4, -1, 6, -1, -1, 9]
Arrangement Rearrangement - Example¶
- Input :
arr = {19, 7, 0, 3, 18, 15, 12, 6, 1, 8, 11, 10, 9, 5, 13, 16, 2, 14, 17, 4} - Output :
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
Arrangement Rearrangement - Naive Approach¶
- Navigate the numbers from 0 to n-1.
- Now navigate through array.
- If (i==a[j]) , then replace the element at i position with a[j] position.
- If there is any element in which -1 is used instead of the number then it will be replaced automatically.
- Now, iterate through the array and check if (a[i]!=i) , if it s true then replace a[i] with -1.
Arrangement Rearrangement in C¶
// C program for above approach
#include <stdio.h>
// Function to transform the array
void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i) {
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
¶
// C program for above approach
#include <stdio.h>
// Function to transform the array
void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i) {
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
Arrangement Rearrangement in C¶
...
// Iterate over array
for (i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
¶
...
// Iterate over array
for (i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
Arrangement Rearrangement in C¶
...
// Print the output
printf("Array after Rearranging\n");
for (i = 0; i < n; i++) {
printf("%d ",ar[i]);
}
}
...
¶
...
// Print the output
printf("Array after Rearranging\n");
for (i = 0; i < n; i++) {
printf("%d ",ar[i]);
}
}
...
Arrangement Rearrangement in C¶
// Driver Code
int main()
{
int n, ar[] = { -1, -1, 6, 1, 9, 3, 2, -1, 4, -1 };
n = sizeof(ar) / sizeof(ar[0]);
// Function Call
fixArray(ar, n);
}
Arrangement Rearrangement in C++¶
// C++ program for above approach
#include <iostream>
using namespace std;
// Function to transform the array
void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i) {
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
Arrangement Rearrangement in C++¶
// Iterate over array
for (i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
Arrangement Rearrangement in C++¶
...
// Print the output
cout << "Array after Rearranging" << endl;
for (i = 0; i < n; i++) {
cout << ar[i] << " ";
}
}
...
Arrangement Rearrangement in C++¶
...
// Driver Code
int main()
{
int n, ar[] = { -1, -1, 6, 1, 9, 3, 2, -1, 4, -1 };
n = sizeof(ar) / sizeof(ar[0]);
// Function Call
fixArray(ar, n);
}
¶
...
// Driver Code
int main()
{
int n, ar[] = { -1, -1, 6, 1, 9, 3, 2, -1, 4, -1 };
n = sizeof(ar) / sizeof(ar[0]);
// Function Call
fixArray(ar, n);
}
Arrangement Rearrangement in Java¶
// Java program for above approach
class GFG{
// Function to transform the array
public static void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for(i = 0; i < n; i++)
{
for(j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i)
{
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
¶
// Java program for above approach
class GFG{
// Function to transform the array
public static void fixArray(int ar[], int n)
{
int i, j, temp;
// Iterate over the array
for(i = 0; i < n; i++)
{
for(j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i)
{
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
...
Arrangement Rearrangement in Java¶
...
// Iterate over array
for(i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
¶
...
// Iterate over array
for(i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
...
Arrangement Rearrangement in Java¶
...
// Print the output
System.out.println("Array after Rearranging");
for(i = 0; i < n; i++)
{
System.out.print(ar[i] + " ");
}
}
...
¶
...
// Print the output
System.out.println("Array after Rearranging");
for(i = 0; i < n; i++)
{
System.out.print(ar[i] + " ");
}
}
...
Arrangement Rearrangement in Java¶
...
// Driver Code
public static void main(String[] args)
{
int n, ar[] = { -1, -1, 6, 1, 9,
3, 2, -1, 4, -1 };
n = ar.length;
// Function Call
fixArray(ar, n);
}
}
Arrangement Rearrangement in C¶
// C# program for above approach
using System;
class GFG {
// Function to transform the array
static void fixArray(int[] ar, int n)
{
int i, j, temp;
// Iterate over the array
for(i = 0; i < n; i++)
{
for(j = 0; j < n; j++)
{
// Check is any ar[j]
// exists such that
// ar[j] is equal to i
if (ar[j] == i)
{
temp = ar[j];
ar[j] = ar[i];
ar[i] = temp;
break;
}
}
}
// Iterate over array
for(i = 0; i < n; i++)
{
// If not present
if (ar[i] != i)
{
ar[i] = -1;
}
}
// Print the output
Console.WriteLine("Array after Rearranging");
for(i = 0; i < n; i++)
{
Console.Write(ar[i] + " ");
}
}
...
Arrangement Rearrangement in C¶
static void Main() {
int[] ar = { -1, -1, 6, 1, 9,
3, 2, -1, 4, -1 };
int n = ar.Length;
// Function Call
fixArray(ar, n);
}
}
// This code is contributed by divyeshrabadiya07
Array Searching and Sorting¶
Difference between Searching and Sorting Algorithm¶
| S.No. | Searching Algorithm | Sorting Algorithm |
|---|---|---|
| 1. | Searching Algorithms are designed to retrieve an element from any data structure where it is used. | A Sorting Algorithm is used to arranging the data of list or array into some specific order. |
| 2. | These algorithms are generally classified into two categories i.e. Sequential Search and Interval Search. | There are two different categories in sorting. These are Internal and External Sorting. |
| 3. | The worst-case time complexity of searching algorithm is O(N). | The worst-case time complexity of many sorting algorithms like Bubble Sort, Insertion Sort, Selection Sort, and Quick Sort is O(N2). |
| 4. | There is no stable and unstable searching algorithms. | Bubble Sort, Insertion Sort, Merge Sort etc are the stable sorting algorithms whereas Quick Sort, Heap Sort etc are the unstable sorting algorithms. |
| 5. | The Linear Search and the Binary Search are the examples of Searching Algorithms. | The Bubble Sort, Insertion Sort, Selection Sort, Merge Sort, Quick Sort etc are the examples of Sorting Algorithms. |
Matrix¶
- Geeks for Geeks
- Matrix Archives - GeeksforGeeks
- CE100 Algorithms and Programming II - RTEU CE100 Algorithms and Programming-II Course Notes
Matrix Rotation - Examples¶
- Given a matrix, clockwise rotate elements in it
- Input
- Output
Matrix Rotation - Examples¶
For 4*4 matrix
- Input
Output:
Matrix Rotation - Examples¶
- The idea is to use loops similar to the program for printing a matrix in spiral form.
- One by one rotate all rings of elements, starting from the outermost.
- To rotate a ring, we need to do following.
-
- Move elements of top row.
-
- Move elements of last column.
-
- Move elements of bottom row.
-
- Move elements of first column.
-
- Repeat above steps for inner ring while there is an inner ring.
Matrix Rotation in C++¶
// C++ program to rotate a matrix
#include <bits/stdc++.h>
#define R 4
#define C 4
using namespace std;
...
Matrix Rotation in C++¶
...
// A function to rotate a matrix mat[][] of size R x C.
// Initially, m = R and n = C
void rotatematrix(int m, int n, int mat[R][C])
{
int row = 0, col = 0;
int prev, curr;
/*
row - Starting row index
m - ending row index
col - starting column index
n - ending column index
i - iterator
*/
while (row < m && col < n)
{
if (row + 1 == m || col + 1 == n)
break;
// Store the first element of next row, this
// element will replace first element of current
// row
prev = mat[row + 1][col];
/* Move elements of first row from the remaining rows */
for (int i = col; i < n; i++)
{
curr = mat[row][i];
mat[row][i] = prev;
prev = curr;
}
row++;
/* Move elements of last column from the remaining columns */
for (int i = row; i < m; i++)
{
curr = mat[i][n-1];
mat[i][n-1] = prev;
prev = curr;
}
n--;
/* Move elements of last row from the remaining rows */
if (row < m)
{
for (int i = n-1; i >= col; i--)
{
curr = mat[m-1][i];
mat[m-1][i] = prev;
prev = curr;
}
}
m--;
/* Move elements of first column from the remaining rows */
if (col < n)
{
for (int i = m-1; i >= row; i--)
{
curr = mat[i][col];
mat[i][col] = prev;
prev = curr;
}
}
col++;
}
...
Matrix Rotation in C++¶
...
// Print rotated matrix
for (int i=0; i<R; i++)
{
for (int j=0; j<C; j++)
cout << mat[i][j] << " ";
cout << endl;
}
}
Matrix Rotation in C++¶
/* Driver program to test above functions */
int main()
{
// Test Case 1
int a[R][C] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
// Test Case 2
/* int a[R][C] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
*/
rotatematrix(R, C, a);
return 0;
}
Matrix Rotation in Java¶
// Java program to rotate a matrix
import java.lang.*;
import java.util.*;
class GFG
{
static int R = 4;
static int C = 4;
// A function to rotate a matrix
// mat[][] of size R x C.
// Initially, m = R and n = C
static void rotatematrix(int m,
int n, int mat[][])
{
int row = 0, col = 0;
int prev, curr;
/*
row - Starting row index
m - ending row index
col - starting column index
n - ending column index
i - iterator
*/
while (row < m && col < n)
{
if (row + 1 == m || col + 1 == n)
break;
// Store the first element of next
// row, this element will replace
// first element of current row
prev = mat[row + 1][col];
// Move elements of first row
// from the remaining rows
for (int i = col; i < n; i++)
{
curr = mat[row][i];
mat[row][i] = prev;
prev = curr;
}
row++;
// Move elements of last column
// from the remaining columns
for (int i = row; i < m; i++)
{
curr = mat[i][n-1];
mat[i][n-1] = prev;
prev = curr;
}
n--;
// Move elements of last row
// from the remaining rows
if (row < m)
{
for (int i = n-1; i >= col; i--)
{
curr = mat[m-1][i];
mat[m-1][i] = prev;
prev = curr;
}
}
m--;
// Move elements of first column
// from the remaining rows
if (col < n)
{
for (int i = m-1; i >= row; i--)
{
curr = mat[i][col];
mat[i][col] = prev;
prev = curr;
}
}
col++;
}
// Print rotated matrix
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
System.out.print( mat[i][j] + " ");
System.out.print("\n");
}
}
Matrix Rotation in Java¶
/* Driver program to test above functions */
public static void main(String[] args)
{
// Test Case 1
int a[][] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
// Test Case 2
/* int a[][] = new int {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};*/
rotatematrix(R, C, a);
}
}
Matrix Rotation in C¶
// C# program to rotate a matrix
using System;
class GFG {
static int R = 4;
static int C = 4;
// A function to rotate a matrix
// mat[][] of size R x C.
// Initially, m = R and n = C
static void rotatematrix(int m,
int n, int [,]mat)
{
int row = 0, col = 0;
int prev, curr;
/*
row - Starting row index
m - ending row index
col - starting column index
n - ending column index
i - iterator
*/
while (row < m && col < n)
{
if (row + 1 == m || col + 1 == n)
break;
// Store the first element of next
// row, this element will replace
// first element of current row
prev = mat[row + 1, col];
// Move elements of first row
// from the remaining rows
for (int i = col; i < n; i++)
{
curr = mat[row,i];
mat[row, i] = prev;
prev = curr;
}
row++;
// Move elements of last column
// from the remaining columns
for (int i = row; i < m; i++)
{
curr = mat[i,n-1];
mat[i, n-1] = prev;
prev = curr;
}
n--;
// Move elements of last row
// from the remaining rows
if (row < m)
{
for (int i = n-1; i >= col; i--)
{
curr = mat[m-1,i];
mat[m-1,i] = prev;
prev = curr;
}
}
m--;
// Move elements of first column
// from the remaining rows
if (col < n)
{
for (int i = m-1; i >= row; i--)
{
curr = mat[i,col];
mat[i,col] = prev;
prev = curr;
}
}
col++;
}
// Print rotated matrix
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
Console.Write( mat[i,j] + " ");
Console.Write("\n");
}
}
Matrix Rotation in C¶
/* Driver program to test above functions */
public static void Main()
{
// Test Case 1
int [,]a = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
// Test Case 2
/* int a[][] = new int {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};*/
rotatematrix(R, C, a);
}
}
// This code is contributed by nitin mittal.
Sparse Matrix¶
- Geeks for Geeks
- Data Structures Tutorials - Sparse Matrix with an example
What is Sparse Matrix?¶
- In computer programming, a matrix can be defined with a 2-dimensional array.
- Any array with 'm' columns and 'n' rows represent a m X n matrix.
- There may be a situation in which a matrix contains more number of ZERO values than NON-ZERO values.
- Such matrix is known as sparse matrix.
- Sparse matrix is a matrix which contains very few non-zero elements.
What is Sparse Matrix?¶
- When a sparse matrix is represented with a 2-dimensional array,
- we waste a lot of space to represent that matrix.
- For example, consider a matrix of size 100 X 100 containing only 10 non-zero elements. In this matrix,
- only 10 spaces are filled with non-zero values and remaining spaces of the matrix are filled with zero.
- That means, totally we allocate 100 X 100 X 2 = 20000 bytes of space to store this integer matrix.
- And to access these 10 non-zero elements we have to make scanning for 10000 times.
- we waste a lot of space to represent that matrix.
- To make it simple we use the following sparse matrix representation.
Sparse Matrix Representations¶
- A sparse matrix can be represented by using TWO representations, those are as follows
- Triplet Representation (Array Representation)
- Linked Representation
Sparse Matrix - Triplet Representation (Array Representation)¶
- In this representation, we consider only non-zero values along with their row and column index values.
- In this representation, the 0th row stores the total number of rows,
- total number of columns and the total number of non-zero values in the sparse matrix.
Sparse Matrix - Triplet Representation (Array Representation)¶
- For example, consider a matrix of size
5 x 6containing6number of non-zero values. This matrix can be represented as shown in the image

Sparse Matrix - Triplet Representation (Array Representation)¶
- In above example matrix, there are only
6non-zero elements ( those are9, 8, 4, 2, 5 & 2) and matrix size is5 X 6. - We represent this matrix as shown in the above image.
- Here the first row in the right side table is filled with values 5, 6 & 6 which indicates that it is a sparse matrix with
5rows,6columns &6non-zero values. - The second row is filled with
0, 4, & 9which indicates the non-zero value 9 is at the 0th-row 4th column in the Sparse matrix. - In the same way, the remaining non-zero values also follow a similar pattern.
Sparse Matrix - Triplet Representation (Array Representation) in C++¶
#include<iostream>
using namespace std;
int main()
{
// sparse matrix of class 5x6 with 6 non-zero values
int sparseMatrix[5][6] =
{
{0 , 0 , 0 , 0 , 9, 0 },
{0 , 8 , 0 , 0 , 0, 0 },
{4 , 0 , 0 , 2 , 0, 0 },
{0 , 0 , 0 , 0 , 0, 5 },
{0 , 0 , 2 , 0 , 0, 0 }
};
...
Sparse Matrix - Triplet Representation (Array Representation) in C++¶
...
// Finding total non-zero values in the sparse matrix
int size = 0;
for (int row = 0; row < 5; row++)
for (int column = 0; column < 6; column++)
if (sparseMatrix[row][column] != 0)
size++;
...
Sparse Matrix - Triplet Representation (Array Representation) in C++¶
...
// Defining result Matrix
int resultMatrix[3][size];
// Generating result matrix
int k = 0;
for (int row = 0; row < 5; row++)
for (int column = 0; column < 6; column++)
if (sparseMatrix[row][column] != 0)
{
resultMatrix[0][k] = row;
resultMatrix[1][k] = column;
resultMatrix[2][k] = sparseMatrix[row][column];
k++;
}
...
Sparse Matrix - Triplet Representation (Array Representation) in C++¶
...
// Displaying result matrix
cout<<"Triplet Representation : "<<endl;
for (int row=0; row<3; row++)
{
for (int column = 0; column<size; column++)
cout<<resultMatrix[row][column]<<" ";
cout<<endl;
}
return 0;
}
Output¶

Sparse Matrix - Linked List Representation¶
- In linked representation, we use a linked list data structure to represent a sparse matrix.
- In this linked list, we use two different nodes namely header node and element node.
Sparse Matrix - Linked List Representation¶
- Header node consists of three fields and element node consists of five fields as shown in the image

Sparse Matrix - Linked List Representation¶
- Consider the above same sparse matrix used in the Triplet representation. This sparse matrix can be represented using linked representation as shown in the below image...

Sparse Matrix - Linked List Representation¶
- In the above representation,
H0, H1,..., H5indicates the header nodes which are used to represent indexes. - Remaining nodes are used to represent non-zero elements in the matrix,
- except the very first node which is used to represent abstract information of the sparse matrix (i.e., It is a matrix of 5 X 6 with 6 non-zero elements).
- In this representation, in each row and column, the last node right field points to its respective header node.
